【题目】已知抛物线C1:y=﹣ ![]() x2+bx+c的对称轴是x=2,且经过点(6,0).
x2+bx+c的对称轴是x=2,且经过点(6,0).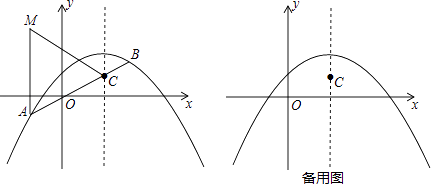
(1)求抛物线C1的解析式;
(2)将抛物线C1向下平移2个单位后得到抛物线C2 , 如图,直线y=kx﹣2k+1交抛物线C2于A,B两点(点A在点B的左边),交抛物线C2的对称轴于点C,M(xA , 3),xA表示点A横坐标,求证:AC=AM;
(3)在(2)的条件下,请你参考(2)中的结论解决下列问题:
①若CM=AM,求 ![]() 的值;
的值;
②请你探究:在抛物线C2上是否存在点P,使得PO+PC取得最小值?如果存在,求出点P的坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)解:∵抛物线C1的对称轴为直线x=2,且抛物线与x轴的一个交点坐标为(6,0),
∴抛物线与x轴的另一个交点坐标为(﹣2,0),
∴抛物线C1的解析式为y=﹣ ![]() (x+2)(x﹣6),
(x+2)(x﹣6),
即y=﹣ ![]() x2+x+3
x2+x+3
(2)证明:∵抛物线C1的解析式为y=﹣ ![]() (x﹣2)2+4,
(x﹣2)2+4,
∴抛物线C2的解析式为y=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
∵直线y=kx﹣2k+1过定点(2,1),
而直线y=kx﹣2k+1交抛物线C2的对称轴于点C,
∴C(2,1),
设A[x,﹣ ![]() (x﹣2)2+2)],
(x﹣2)2+2)],
∴AC2=(x﹣2)2+[﹣ ![]() (x﹣2)2+2﹣1]2=
(x﹣2)2+2﹣1]2= ![]() (x﹣2)4+
(x﹣2)4+ ![]() (x﹣2)2+1,
(x﹣2)2+1,
AM2=[﹣ ![]() (x﹣2)2+2﹣3]2=
(x﹣2)2+2﹣3]2= ![]() (x﹣2)4+
(x﹣2)4+ ![]() (x﹣2)2+1,
(x﹣2)2+1,
∴AC=AM
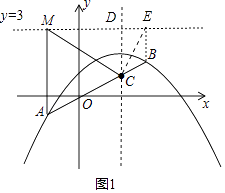
(3)解:①∵AC=AM,CM=AM,
∴△ACM是等边三角形.
∴∠AMC=∠ACM=60°,
直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,如图1,则由(2)可知BC=BE,易证∠MCD=60°,∠BCE=∠DCE=30°,
在Rt△CDE中,tan∠DCE=tan30°= ![]() =
= ![]() ,
,
在Rt△CDM中,tan∠CMD=tan30°= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AM∥DC∥EB,
∴ ![]() =
= ![]() =
= ![]() ;
;
②存在.
如图2,y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,
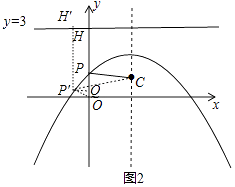
由(2)可知PC=PH,
如图,在抛物线上取异于点P的P′,作P′H′⊥直线y=3于H′,P′Q⊥y轴于点Q,
由(2)可知P′C=PH′,
易得四边形HH′P′Q为矩形,
∴P′H′=QH,
∵OP′>OQ,
∴OQ+QH<OP′+P′H′,
∴OP+PH<OP′+P′C,
∴点P(0,1)使得PO+PC取得最小值.
【解析】(1)根据已知点的坐标和对称轴求出此抛物线与x轴的另一个交点坐标,即可求出抛物线的解析式。
(2)先抛物线C1写成顶点式,再根据平移规律(上加下减),求出抛物线C2的函数解析式,而交抛物线C2的对称轴于点C,,可知点C(2,1),再设出点A的坐标,利用勾股定理求出AC2、AM2即可得到AC=AM。
(3)①由已知易征得△ACM是等边三角形.直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,在Rt△CDE中和Rt△CDM中,利用解直角三角形得出![]() 、
、![]() 的值,从而得到DE:DM的值,再由AM∥DC∥EB,得出对应线段成比例,即可求得结果;②y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,先证明四边形HH′P′Q为矩形,得到P′H′=QH,再利用OP′>OQ得出OP+PH<OP′+P′C,,于是可判断点P(0,1)使得PO+PC取得最小值。
的值,从而得到DE:DM的值,再由AM∥DC∥EB,得出对应线段成比例,即可求得结果;②y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,先证明四边形HH′P′Q为矩形,得到P′H′=QH,再利用OP′>OQ得出OP+PH<OP′+P′C,,于是可判断点P(0,1)使得PO+PC取得最小值。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如下的三角形解释(a+b)n的展开式中各项的系数,此三角形称为“杨辉三角”,
即:(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
根据“杨辉三角”计算出(a+b)10的展开式中第三项的系数为( )
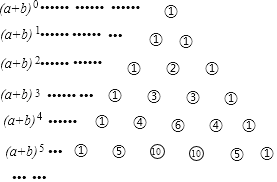
A.10B.45C.46D.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
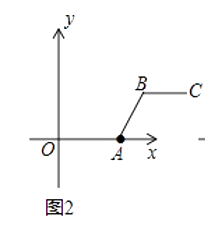
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;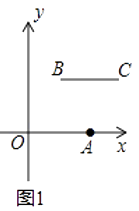
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.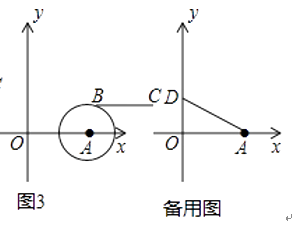
(3)当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1)所示,已知
 中,
中, 试确定
试确定
(2)如图(2)所示,已知
 中,
中, 试确定
试确定
(3)如图(3)所示,已知
 中,
中, 试确定
试确定


-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣2a3b(﹣4a2b)÷6a4b2
(2)

(3)

(4)(2a﹣1)(a﹣4)﹣(a+3)(a﹣4)
(5)(x﹣3y+4)(x+3y﹣4)
(6)(a+2b)(a﹣2b)(a2﹣4b2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
,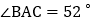 ,
,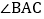 的平分线与AB的垂直平分线交于点O,将
的平分线与AB的垂直平分线交于点O,将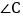 沿EF折叠,若点C与点O恰好重合,则
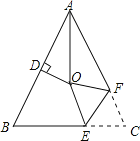
沿EF折叠,若点C与点O恰好重合,则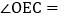 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
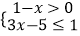 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.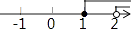
B.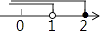
C.
D.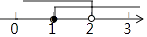
相关试题

