【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.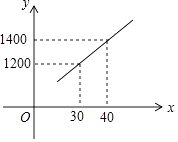
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
参考答案:
【答案】
(1)解:设y2与x的函数关系式为y2=kx+b,
![]() ,得
,得 ![]() ,
,
∴y2与x之间的函数关系式是y2=20x+600
(2)解:由题意可得, ![]() ,
,
解得,25≤x≤40,
即月产量x的取值范围是25≤x≤34
(3)解:由题意可得,
W=xy1﹣y2=x(160﹣20x)﹣20x﹣600,
=﹣2(x﹣35)2+1850,
∵25≤x≤40,
∴x=35时,W取得最大值,此时W=1850,
即当月产量x(套)为35套时,这种产品的利润W(万元)最大,最大利润是2650万元
【解析】(1)观察图像,y2与x是一次函数,代入图像上的两点坐标,即可求出函数解析式。
(2)找出题中的不等关系:每套产品的生产成本≤44万元,每套产品的售价≥80万元。列出不等式组求解,即可求出x的取值范围
(3)先求出W与x的函数解析式,求出顶点坐标,即可求出结果。
【考点精析】通过灵活运用一元一次不等式组的解法和确定一次函数的表达式,掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.

(1)求证:AC平分∠FAD;
(2)已知AF=3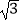 ,求阴影部分面积.
,求阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,数轴上的点A,B.C依次表示数-2,x,4.某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点B,发现点A对齐刻度1.8cm,点C对齐刻度5.4cm.
(1)AC= 个单位长度;由图可知数轴上的一个单位长度对应刻度尺上的 cm;数轴上的点B表示数 ;

(2)已知T是数轴上一点(不与点A、点B、点C重合),点P表示的数是t,点P是线段BT的三等分点,且TP=2BP.
①如图3,当-2<t<4时,试试猜想线段CT与AP的数量关系,并说明理由;
②若|2BT-3AP|=1,请直接写出所有满足条件的t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点B在线段AC上,点D在线段AB上.
(1)如图1,若AB=6cm,BC=4cm,D为线段AC的中点,求线段DB的长度;
(2)如图2,若BD=
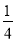 AB=
AB=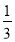 CD,E为线段AB的中点,EC=12cm,求线段AC的长度.
CD,E为线段AB的中点,EC=12cm,求线段AC的长度.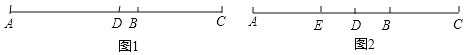
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般地,
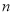 个相同的因数
个相同的因数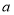 相乘
相乘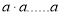 ,记为
,记为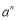 , 如
, 如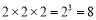 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为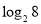 (即
(即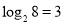 ) .一般地,若
) .一般地,若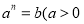 且
且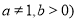 , 则
, 则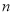 叫做以
叫做以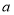 为底
为底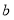 的对数, 记为
的对数, 记为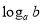 (即
(即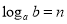 ) .如
) .如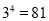 , 则4叫做以3为底81的对数, 记为
, 则4叫做以3为底81的对数, 记为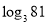 (即
(即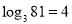 ) .
) .(1)计算下列各对数的值:
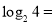 ;
;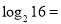 ;
;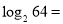 .
.(2)观察(1)中三数4、16、64之间满足怎样的关系式,
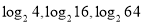 之间又满足怎样的关系式;
之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?
(4) 根据幂的运算法则:
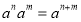 以及对数的含义说明上述结论.
以及对数的含义说明上述结论. -
科目: 来源: 题型:
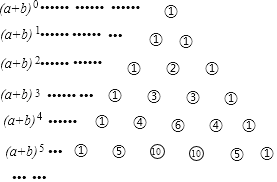
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如下的三角形解释(a+b)n的展开式中各项的系数,此三角形称为“杨辉三角”,
即:(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
根据“杨辉三角”计算出(a+b)10的展开式中第三项的系数为( )
A.10B.45C.46D.50
相关试题

