【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

参考答案:
【答案】见解析
【解析】试题分析:(1)由于D是BC的中点,那么BD=CD,而BE=CF,DE⊥AB,DF⊥AC,利用HL易证![]() ,可得DE=DF,利用角平分线的判定定理可知点点D在∠BAC的平分线上,即AD平分∠BAC;
,可得DE=DF,利用角平分线的判定定理可知点点D在∠BAC的平分线上,即AD平分∠BAC;
(2)根据全等三角形的性质即可得到结论.
试题解析:
(1)∵D是BC的中点
∴BD=CD,
又∵BE=CF,DE⊥AB,DF⊥AC,
![]()
∴DE=DF,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC;
(2) ![]()
∴∠B=∠C,
∴AB=AC,
∵BE=CF,
∴ABBE=ACCF,
∴AE=AF,
∵DE=DF,
∴AD垂直平分EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=33°,则∠CAD= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数的图象经过点(﹣2,6),那么这个函数中的函数值y随自变量x值的增大而_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程ax2﹣bx﹣2015=0有一根为x=﹣1,则a+b= .
-
科目: 来源: 题型:
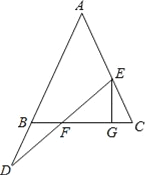
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形,并探究和解答下列问题:

(1)设铺设地面所用瓷砖的总块数为y,请写出y与n(表示第n个图形)的关系式;
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明
-
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A.4
B.±4
C.8
D.±8
相关试题

