【题目】如图,点![]() 是正方形
是正方形![]() 边
边![]() 上一点,连接
上一点,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 手点
手点![]() ,连接
,连接![]() .
.
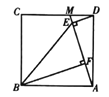
(1)求证:![]() ;
;
(2已知![]() ,四边形
,四边形![]() 的面积为24,求
的面积为24,求![]() 的正弦值.
的正弦值.
参考答案:
【答案】(1)证明见解析;(2)![]()
![]() .
.
【解析】(1)通过证明△ABF≌△DEA得到BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到![]() xx+
xx+![]() x2=24,解方程求出x得到AE=BF=6,则EF=x-2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
x2=24,解方程求出x得到AE=BF=6,则EF=x-2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
详(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DEA中
 ,
,
∴△ABF≌△DEA(AAS),
∴BF=AE;
(2)解:设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴![]() xx+
xx+![]() x2=24,解得x1=6,x2=-8(舍去),
x2=24,解得x1=6,x2=-8(舍去),
∴EF=x-2=4,
在Rt△BEF中,BE=![]() ,
,
∴sin∠EBF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新规定:点
 为线段
为线段 上一点,当
上一点,当 或
或 时,我们就规定
时,我们就规定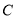 为线段
为线段 的“三倍距点”。如图,在数轴上,点
的“三倍距点”。如图,在数轴上,点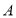 所表示的数为-3,点
所表示的数为-3,点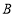 所表示的数为5.
所表示的数为5.
(1)确定点
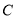 所表示的数为___________.
所表示的数为___________.(2)若动点
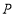 从点
从点 出发,沿射线
出发,沿射线 方向以每秒2个单位长度的速度运动,设运动时间为
方向以每秒2个单位长度的速度运动,设运动时间为 秒.
秒.①当点
 与点
与点 重合时,求
重合时,求 的值.
的值.②求
 的长度(用含
的长度(用含 的代数式表示).
的代数式表示).③当点
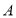 为线段
为线段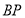 的“三倍距点”时,直接写出
的“三倍距点”时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的有( )
①
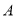 是
是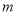 次多项式,
次多项式,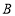 是
是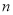 次多项式(
次多项式(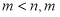 和
和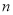 都是正整数),则
都是正整数),则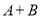 和
和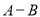 一定都是
一定都是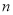 次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③
次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③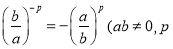 为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变
为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变A.
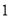 个B.
个B.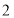 个C.
个C.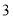 个D.
个D.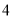 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式
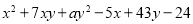 可分解为两个一次因式的积,则
可分解为两个一次因式的积,则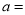 ______________.
______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.
(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
-
科目: 来源: 题型:
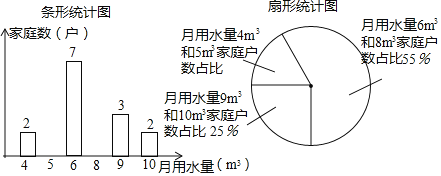
查看答案和解析>>【题目】如图,直线
 与
与 轴交于点
轴交于点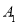 ,依次作正方形
,依次作正方形 、正方形
、正方形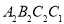 、…正方形
、…正方形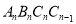 使得点
使得点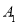 、
、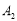 、…,
、…,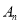 在直线
在直线 上,点
上,点 、
、 、…,
、…, 在
在 轴上,则点
轴上,则点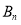 的坐标是( )
的坐标是( )
A.
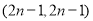 B.
B. 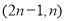
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2
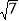 ,AC=2
,AC=2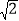 ,求AD的长.
,求AD的长.
相关试题

