【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.
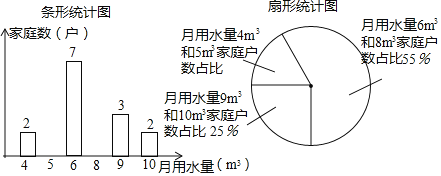
(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
参考答案:
【答案】(1)n=20,补全图形见解析;(2)这20户家庭的月平均用水量为6.95m3,估计小莹所住小区420户家庭中月用水量低于6.95m3的家庭户数为231户;(3)选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率为![]() .
.
【解析】(1)根据月用水量为9m3和10m3的户数及其所占百分比可得总户数,再求出5m3和8m3的户数即可补全图形;
(2)根据加权平均数的定义计算可得月平均用水量,再用总户数乘以样本中低于月平均用水量的家庭户数所占比例可得;
(3)列表得出所有等可能结果,从中找到满足条件的结果数,根据概率公式计算可得.
(1)n=(3+2)÷25%=20,
月用水量为8m3的户数为20×55%-7=4户,
月用水量为5m3的户数为20-(2+7+4+3+2)=2户,
补全图形如下:
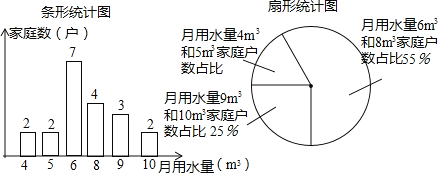
(2)这20户家庭的月平均用水量为![]() =6.95(m3),
=6.95(m3),
因为月用水量低于6.95m3的有11户,
所以估计小莹所住小区420户家庭中月用水量低于6.95m3的家庭户数为420×![]() =231户;
=231户;
(3)月用水量为5m3的两户家庭记为a、b,月用水量为9m3的3户家庭记为c、d、e,
列表如下:
a | b | c | d | e | |
a | (b,a) | (c,a) | (d,a) | (e,a) | |
b | (a,b) | (c,b) | (d,b) | (e,b) | |
c | (a,c) | (b,c) | (d,c) | (e,c) | |
d | (a,d) | (b,d) | (c,d) | (e,d) | |
e | (a,e) | (b,e) | (c,e) | (d,e) |
由表可知,共有20种等可能结果,其中满足条件的共有12种情况,
所以选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的有( )
①
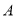 是
是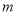 次多项式,
次多项式,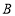 是
是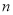 次多项式(
次多项式(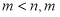 和
和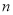 都是正整数),则
都是正整数),则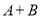 和
和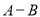 一定都是
一定都是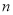 次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③
次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③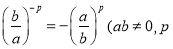 为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变
为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变A.
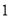 个B.
个B.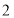 个C.
个C.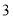 个D.
个D.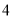 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式
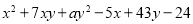 可分解为两个一次因式的积,则
可分解为两个一次因式的积,则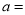 ______________.
______________. -
科目: 来源: 题型:
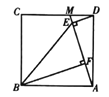
查看答案和解析>>【题目】如图,点
 是正方形
是正方形 边
边 上一点,连接
上一点,连接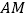 ,作
,作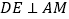 于点
于点 ,
,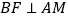 手点
手点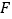 ,连接
,连接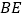 .
.
(1)求证:
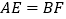 ;
;(2已知
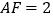 ,四边形
,四边形 的面积为24,求
的面积为24,求 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
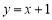 与
与 轴交于点
轴交于点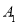 ,依次作正方形
,依次作正方形 、正方形
、正方形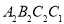 、…正方形
、…正方形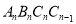 使得点
使得点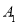 、
、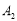 、…,
、…,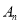 在直线
在直线 上,点
上,点 、
、 、…,
、…, 在
在 轴上,则点
轴上,则点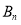 的坐标是( )
的坐标是( )
A.
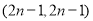 B.
B. 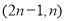
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2
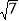 ,AC=2
,AC=2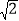 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
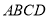 ,点
,点 是线段
是线段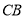 延长线上一点,联结
延长线上一点,联结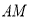 ,其中
,其中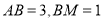 .若将
.若将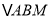 绕着点
绕着点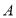 逆时针旋转使得
逆时针旋转使得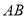 与
与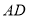 第一次重合时,点
第一次重合时,点 落在点
落在点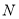 (图中未画出).求:在此过程中,
(图中未画出).求:在此过程中,
(1)
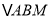 旋转的角度等于 ______________
旋转的角度等于 ______________ .
.(2)线段
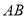 扫过的平面部分的面积为__________(结果保留
扫过的平面部分的面积为__________(结果保留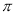 )
)(3)联结
 ,则
,则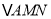 的面积为____________.
的面积为____________.
相关试题

