【题目】已知多项式![]() 可分解为两个一次因式的积,则
可分解为两个一次因式的积,则![]() ______________.
______________.
参考答案:
【答案】-18
【解析】
设原式可分解为(x+ky+c)(x+ly+d),展开后得出x2+(k+l)xy+kly2+(c+d)x+(cl+dk)y+cd,推出cd=-24,c+d=-5,cl+dk=43,k+l=7,a=kl求出即可.
解:∵多项式的第一项是x2,因此原式可分解为:(x+ky+c)(x+ly+d)
∵(x+ky+c)(x+ly+d)= x2+(k+l)xy+kly2+(c+d)x+(cl+dk)y+cd,
∴cd=-24,c+d=-5,
∴c=3,d=-8,
∵cl+dk=43,
∴3l-8k=43,
∵k+l=7,
∴k=-2,l=9,
∴a=kl=-18
故答案为-18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,
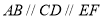 ,试说明
,试说明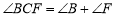 .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
.下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.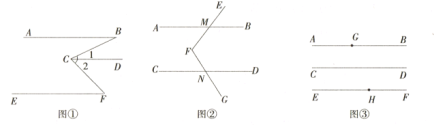
解: ∵
 .(已知)
.(已知)∴
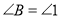 .( )
.( )同理可证,
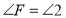 .
.∵
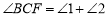 ,
,∴
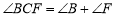 .( )
.( )应用:如图②,
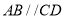 ,点
,点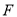 在
在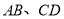 之间,
之间,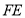 与
与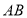 交于点
交于点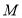 ,
,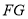 与
与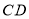 交于点
交于点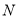 .若
.若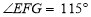 ,
,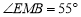 ,则
,则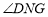 的大小为_____________度.
的大小为_____________度.拓展:如图③,直线
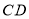 在直线
在直线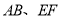 之间,且
之间,且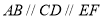 ,点
,点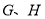 分别在直线
分别在直线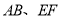 上,点
上,点 是直线
是直线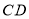 上的一个动点,且不在直线
上的一个动点,且不在直线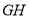 上,连结
上,连结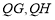 .若
.若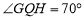 ,则
,则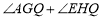 =________度.
=________度. -
科目: 来源: 题型:
查看答案和解析>>【题目】新规定:点
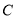 为线段
为线段 上一点,当
上一点,当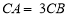 或
或 时,我们就规定
时,我们就规定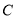 为线段
为线段 的“三倍距点”。如图,在数轴上,点
的“三倍距点”。如图,在数轴上,点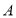 所表示的数为-3,点
所表示的数为-3,点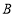 所表示的数为5.
所表示的数为5.
(1)确定点
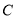 所表示的数为___________.
所表示的数为___________.(2)若动点
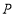 从点
从点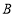 出发,沿射线
出发,沿射线 方向以每秒2个单位长度的速度运动,设运动时间为
方向以每秒2个单位长度的速度运动,设运动时间为 秒.
秒.①当点
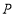 与点
与点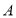 重合时,求
重合时,求 的值.
的值.②求
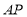 的长度(用含
的长度(用含 的代数式表示).
的代数式表示).③当点
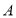 为线段
为线段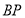 的“三倍距点”时,直接写出
的“三倍距点”时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的有( )
①
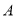 是
是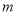 次多项式,
次多项式,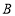 是
是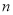 次多项式(
次多项式(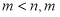 和
和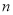 都是正整数),则
都是正整数),则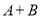 和
和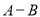 一定都是
一定都是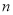 次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③
次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③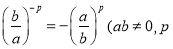 为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变
为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变A.
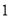 个B.
个B.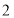 个C.
个C.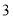 个D.
个D.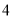 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是正方形
是正方形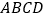 边
边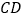 上一点,连接
上一点,连接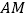 ,作
,作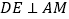 于点
于点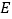 ,
,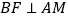 手点
手点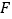 ,连接
,连接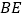 .
.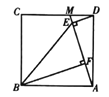
(1)求证:
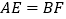 ;
;(2已知
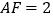 ,四边形
,四边形 的面积为24,求
的面积为24,求 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.
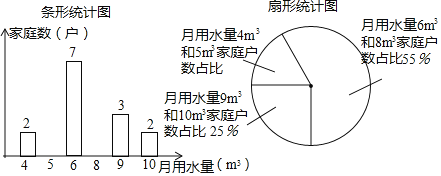
(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
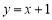 与
与 轴交于点
轴交于点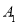 ,依次作正方形
,依次作正方形 、正方形
、正方形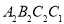 、…正方形
、…正方形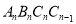 使得点
使得点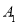 、
、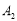 、…,
、…,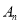 在直线
在直线 上,点
上,点 、
、 、…,
、…, 在
在 轴上,则点
轴上,则点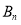 的坐标是( )
的坐标是( )
A.
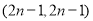 B.
B. 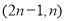
C.
 D.
D. 
相关试题

