【题目】如下图,![]() 中,三条内角平分线
中,三条内角平分线![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() .
.

(1)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.
的度数.
(2)若![]() ,
,![]() ,则
,则![]() 和
和![]() 相等吗?请说明理由.
相等吗?请说明理由.
参考答案:
【答案】(1)50°,50°;(2)相等,理由见解析
【解析】
(1)由于AD、BE、CF为△ABC的角平分线,所以可得∠BAD=∠CAD=30°,∠ABE=∠CBE=20°,∠BCF=∠ACF,根据三角形外角的意义求得∠BOD,进一步利用三角形的内角和得出答案即可;
(2)类比于(1)的方法得出答案即可.
(1)∵![]() ,
,![]() ,AD、BE、CF为△ABC的角平分线,
,AD、BE、CF为△ABC的角平分线,
∴∠BAD=∠CAD=30°,∠ABE=∠CBE=20°,∠BCF=∠ACF,
∴∠BOD=∠OAB+∠OBA=![]() ∠BAC+
∠BAC+![]() ∠ABC=50°
∠ABC=50°
∴∠COG=90°∠OCG=90°![]() (180∠ABC∠BAC)=90°40°=50°.
(180∠ABC∠BAC)=90°40°=50°.
(2)∠BOD和∠COG相等.
理由:∠BOD=∠OAB+∠OBA=![]() ∠BAC+
∠BAC+![]() ∠ABC=
∠ABC=![]() (α+β)=
(α+β)= ![]() (180°∠ACB)=90°
(180°∠ACB)=90°![]() ∠ACB=90°∠OCG=∠COG
∠ACB=90°∠OCG=∠COG
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,反比例函数y=
 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
-
科目: 来源: 题型:
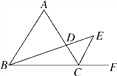
查看答案和解析>>【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
-
科目: 来源: 题型:
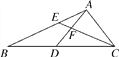
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒
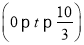 ,连接MN.
,连接MN.(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=
 中,x取x≠-1的实数
中,x取x≠-1的实数C.y=
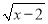 中,x取x≥2的实数
中,x取x≥2的实数D.y=
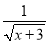 中,x取x≥-3的实数
中,x取x≥-3的实数 -
科目: 来源: 题型:
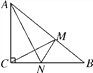
查看答案和解析>>【题目】如下图,
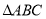 和
和 是等腰直接角三角形,
是等腰直接角三角形,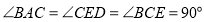 ,点
,点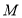 为
为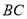 边上一点,连接
边上一点,连接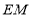 ,
,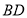 交于点
交于点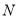 ,点
,点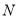 恰好是
恰好是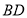 中点,连接
中点,连接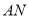 .
.
(1)求证:
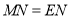 ;
;(2)连接AM、AE,请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
相关试题

