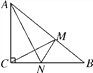
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒![]() ,连接MN.
,连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
参考答案:
【答案】 (1) △BMN与△ABC相似时,t的值为![]() 或
或![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)、根据Rt△ABC的勾股定理得出AB的长度,然后用含t的代数式分别表示BM、CN和BN的长度,然后根据两种不同的相似得出t的值,得出答案;(2)、过点M作MD⊥CB于点D,从而得出△BDM和△BCA相似,从而求出DM、BD和CD的长度,然后根据垂直得出△CAN和△DCM相似,从而得出t的值.
试题解析:(1)∵∠ACB=90°,AC=6cm,BC=8cm, ∴BA=![]() =10(cm).
=10(cm).
由题意得BM=3tcm,CN=2tcm, ∴BN=(8-2t)cm.
当△BMN∽△BAC时,![]() =
=![]() , ∴
, ∴![]() =
=![]() ,解得t=
,解得t=![]() ;
;
当△BMN∽△BCA时,![]() =
=![]() , ∴
, ∴![]() =
=![]() ,解得t=
,解得t=![]() .
.
综上所述,△BMN与△ABC相似时,t的值为![]() 或
或![]() ;
;
(2)如图,过点M作MD⊥CB于点D,
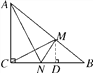
∴∠BDM=∠ACB=90°, 又∵∠B=∠B, ∴△BDM∽△BCA,
∴![]() =
=![]() =
=![]() . ∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
. ∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
∴DM=![]() tcm,BD=
tcm,BD=![]() tcm, ∴CD=
tcm, ∴CD=![]() cm.
cm.
∵AN⊥CM,∠ACB=90°, ∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD. ∵MD⊥CB, ∴∠MDC=∠ACB=90°, ∴△CAN∽△DCM,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得t=
, 解得t=![]() .
.
-
科目: 来源: 题型:
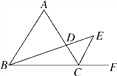
查看答案和解析>>【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
-
科目: 来源: 题型:
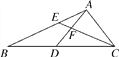
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,
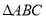 中,三条内角平分线
中,三条内角平分线 相交于点
相交于点 ,
, 于点
于点 .
.
(1)若
 ,
, ,求
,求 和
和 的度数.
的度数.(2)若
 ,
, ,则
,则 和
和 相等吗?请说明理由.
相等吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=
 中,x取x≠-1的实数
中,x取x≠-1的实数C.y=
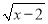 中,x取x≥2的实数
中,x取x≥2的实数D.y=
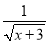 中,x取x≥-3的实数
中,x取x≥-3的实数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,
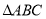 和
和 是等腰直接角三角形,
是等腰直接角三角形,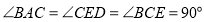 ,点
,点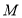 为
为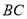 边上一点,连接
边上一点,连接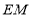 ,
,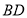 交于点
交于点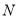 ,点
,点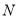 恰好是
恰好是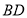 中点,连接
中点,连接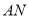 .
.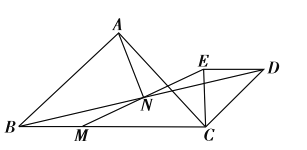
(1)求证:
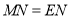 ;
;(2)连接AM、AE,请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

相关试题

