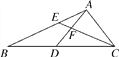
【题目】如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.
参考答案:
【答案】详见解析.
【解析】试题分析:(1)、根据已知条件的线段比值以及∠AEF=∠CEA得出△EAF和△ECA相似,从而得出∠EAF=∠ECA,根据AD=AC得出∠ADC=∠ACD,从而得出角度之间的关系;(2)、根据第一题中的相似得出∠EFA=∠CAB,根据BD=AD得出∠B=∠EAF,从而得出△FAE和△ABC相似,即![]() ,根据AC=AD得出结论.
,根据AC=AD得出结论.
试题解析:(1)∵AE2=EF·EC, ∴![]() =
=![]() , 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
, 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
∴∠EAF=∠ECA. ∵AD=AC, ∴∠ADC=∠ACD.
∵∠ACD=∠DCE+∠ECA=∠DCE+∠EAF, ∴∠ADC=∠DCE+∠EAF;
(2)由(1)可知△EAF∽△ECA, ∴∠EFA=∠EAC, 即∠EFA=∠CAB.
∵BD=AD, ∴∠B=∠BAD,即∠B=∠EAF, ∴△FAE∽△ABC,
∴![]() =
=![]() , ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.
, ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,反比例函数y=
 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
-
科目: 来源: 题型:
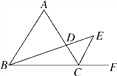
查看答案和解析>>【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,
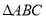 中,三条内角平分线
中,三条内角平分线 相交于点
相交于点 ,
, 于点
于点 .
.
(1)若
 ,
, ,求
,求 和
和 的度数.
的度数.(2)若
 ,
, ,则
,则 和
和 相等吗?请说明理由.
相等吗?请说明理由. -
科目: 来源: 题型:
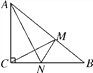
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒
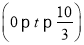 ,连接MN.
,连接MN.(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=
 中,x取x≠-1的实数
中,x取x≠-1的实数C.y=
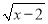 中,x取x≥2的实数
中,x取x≥2的实数D.y=
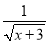 中,x取x≥-3的实数
中,x取x≥-3的实数
相关试题

