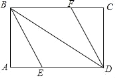
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
(3)在(2)的条件下,当AE=3时,求四边形BEDF的面积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)18![]() .
.
【解析】
(1)由BE、DF均为角平分线可得∠EBD=∠FDB,则BE∥DF,再由题意可知BF∥DE,故利用两组对边分别平行可证明;
(2)菱形的四边相等,则∠ABE=∠EBD=∠EDB,又由∠ABD+∠EDB=90可求解出∠ABE的度数;
(3)分别求解出AB和ED的长度,利用菱形面积公式计算即可.
证明:(1)∵四边形ABCD是矩形
∴AB∥CD,BC∥AD,∠A=90°=∠ABC
∵AB∥CD
∴∠ABD=∠BDC
∵BE,DF分别平分∠ABD,∠BDC
∴∠ABE=∠DBE=![]() ∠ABD,∠CDF=∠BDF=
∠ABD,∠CDF=∠BDF=![]() ∠BDC
∠BDC
∴∠EBD=∠FDB
∴BE∥DF且AD∥BC
∴四边形BEDF为平行四边形
(2)若四边形BEDF是菱形
∴∠CBD=∠DBE,且∠DBE=∠ABE
∴∠CBD=∠DBE=∠ABE
∵∠CBD+∠DBE+∠ABE=90°
∴∠ABE=30°
∴当∠ABE=30°时,四边形BEDF是菱形
(3)∵∠A=90°,∠ABE=30°,AE=3
∴BE=6,AB=![]() AE=3
AE=3![]()
∵四边形BEDF是菱形
∴BE=DE=6
∴四边形BEDF的面积=DE×AB=18![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2).

(1)①将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
②画出△ABC关于x轴对称的△A2B2C2;
③将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△与△成轴对称,对称轴是;△与△成中心对称,对称中心的坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)4
 +
+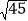 ﹣
﹣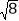 +4
+4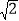
(2)(3
 ﹣2
﹣2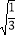 +
+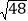 )÷2
)÷2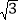
(3)
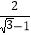 +
+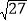 ﹣(
﹣(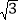 ﹣1)0
﹣1)0(4)
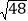 ÷
÷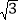 ﹣
﹣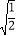 ﹣
﹣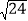
(5)(
 ﹣3)2+(
﹣3)2+(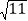 ﹣3)(
﹣3)(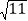 +3)
+3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
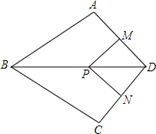
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
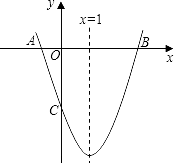
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标. -
科目: 来源: 题型:
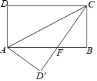
查看答案和解析>>【题目】如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处.
(1)求证:△AFD′≌△CFB;
(2)求线段BF的长度;
(3)试求出重叠部分△AFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
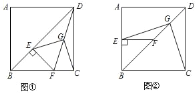
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
相关试题

