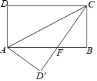
【题目】如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处.
(1)求证:△AFD′≌△CFB;
(2)求线段BF的长度;
(3)试求出重叠部分△AFC的面积.
参考答案:
【答案】(1)见解析;(2)BF=3;(3)10.
【解析】
(1)由翻折的性质可得AD’=CB,再由对顶角可得∠AFD’=∠CFB,再∠D’=∠B=90°,则可证两三角形全等;
(2)设BF为x,则由三角形全等可得CF=AF=8-x,题干已知BC=4,故利用勾股定理BC2+FB2=CF2可求解;
(3)求解出AF长度,以AF为底,BC长度为高,利用三角形面积公式即可求解.
解:(1)由折叠可得,∠D'=∠D=∠B=90°,AD'=AD=BC,
在△AD'F和△CBF中,
∵∠AFD’=∠CFB,∠D’=∠B=90°,AD’=CB,
∴△AFD≌△CFB(AAS);
(2)由折叠可得,∠ACF=∠ACD,
∵CD∥AB,
∴∠CAF=∠ACD,
∴∠ACF=∠CAF,
∴AF=CF,
设BF=x,则AF=CF=8﹣x,
∵∠B=90°,
∴在Rt△BCF中,BF2+CB2=CF2,
即42+x2=(8﹣x)2,
解得x=3,
∴BF=3;
(3)∵AF=8﹣3=5,BC=4,CB⊥AF,
∴S△ACF=![]() AF×BC=
AF×BC=![]() ×5×4=10.
×5×4=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
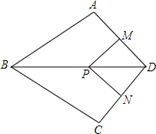
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
-
科目: 来源: 题型:
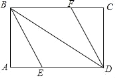
查看答案和解析>>【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
(3)在(2)的条件下,当AE=3时,求四边形BEDF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
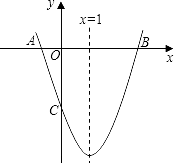
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
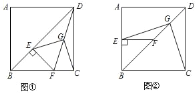
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+m(m≠0)与反比例函数
 的图象在同一平面直角坐标系中是( )
的图象在同一平面直角坐标系中是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
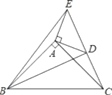
A. 1 B. 2 C. 3 D. 4
相关试题

