搜索
【题目】计算：
（1）4
+
﹣
+4
（2）（3
﹣2
+
）÷2
（3）
+
﹣（﹣1）0
（4）÷﹣
﹣
（5）（﹣3）2+（
﹣3）（+3）
参考答案：
【答案】（1）7
+2
；（2）
；（3）4
；（4）4﹣
﹣2
；（5）16﹣6．
【解析】
(1)先将二次根式化为最简二次根式，然后合并计算即可；
(2)展开括号，按照二次根式混合运算顺序计算；
(3)将各二次根式化为最简二次根式后按照二次根式混合运算顺序计算，任何数的零次方都为1；
(4)按照二次根式混合运算顺序计算，注意最后结果二次根式要化为最简；
(5)分别展开完全平方公式和运用平方差公式去括号，然后再按照二次根式混合运算顺序计算.
解：（1）原式=
；
（2）原式=
；
（3）原式=
；
（4）原式=
；
（5）原式=5﹣6+9+11﹣9=16﹣6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把抛物线y=
x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y= x2交于点Q，则图中阴影部分的面积为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=
BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE=
BC，成立的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，A（﹣2，3），B（﹣3，1），C（﹣1，2）．
（1）①将△ABC向右平移4个单位长度，画出平移后的△A1B1C1；
②画出△ABC关于x轴对称的△A2B2C2；
③将△ABC绕原点O旋转180°，画出旋转后的△A3B3C3；
（2）在△A1B1C1 ， △A2B2C2 ， △A3B3C3中，△与△成轴对称，对称轴是；△与△成中心对称，对称中心的坐标是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分ABC，P是BD上一点，过点P作PM^AD，PN^CD，垂足分别为M、N。
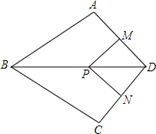
（1）求证：ADB=CDB；
（2）若ADC=90°，求证：四边形MPND是正方形。
-
科目： 来源： 题型：
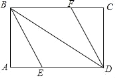
查看答案和解析>>【题目】如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．
（1）求证：四边形BEDF为平行四边形；
（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．
（3）在（2）的条件下，当AE=3时，求四边形BEDF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（﹣1，0）、C（0，﹣3）两点，与x轴交于另一点B．
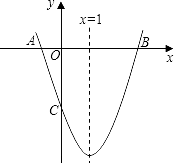
（1）求这条抛物线所对应的函数关系式；
（2）在抛物线的对称轴x=1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标．
相关试题
