【题目】已知函数y= 的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：
①若点M1（x1 ， y1），M2（x2 ， y2）在图象上，且x1＜x2＜0，则y1＜y2；
②当点P坐标为（0，﹣3）时，△AOB是等腰三角形；
③无论点P在什么位置，始终有S△AOB=7.5，AP=4BP；
④当点P移动到使∠AOB=90°时，点A的坐标为（2 ，﹣ ）．
其中正确的结论个数为（ ）

A.1
B.2
C.3
D.4

参考答案：

【答案】C
【解析】解：①错误．∵x1＜x2＜0，函数y随x是增大而减小，∴y1＞y2 ， 故①错误．
②正确．∵P（0，﹣3），
∴B（﹣1，﹣3），A（4，﹣3），
∴AB=5，OA= =5，
∴AB=AO，
∴△AOB是等腰三角形，故②正确．
③正确．设P（0，m），则B（ ，m），A（﹣ ，m），
∴PB=﹣ ，PA=﹣ ，
∴PA=4PB，
∵SAOB=S△OPB+S△OPA= + =7.5，故③正确．
④正确．设P（0，m），则B（ ，m），A（﹣ ，m），
∴PB=﹣ ，PA=﹣ ，OP=﹣m，
∵∠AOB=90°，∠OPB=∠OPA=90°，
∴∠BOP+∠AOP=90°，∠AOP+∠OPA=90°，
∴∠BOP=∠OAP，
∴△OPB∽△APO，
∴ = ，
∴OP2=PBPA，
∴m2=﹣ （﹣ ），
∴m4=36，
∵m＜0，
∴m=﹣ ，
∴A（2 ，﹣ ），故④正确．
∴②③④正确，
故选C．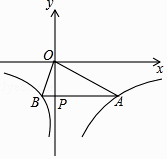

【考点精析】根据题目的已知条件，利用一次函数的性质和等腰三角形的判定的相关知识可以得到问题的答案，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．

关闭