【题目】如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
A.2017π
B.2034π
C.3024π
D.3026π
参考答案:
【答案】D
【解析】解:∵AB=4,BC=3,
∴AC=BD=5,
转动一次A的路线长是: ![]() =2π,
=2π,
转动第二次的路线长是: ![]() =
= ![]() π,
π,
转动第三次的路线长是: ![]() =
= ![]() π,
π,
转动第四次的路线长是:0,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为: ![]() π+
π+ ![]() π+2π=6π,
π+2π=6π,
∵2017÷4=504…1,
∴顶点A转动四次经过的路线长为:6π×504+2π=3026π,
故选D.
【考点精析】利用弧长计算公式和图形的旋转对题目进行判断即可得到答案,需要熟知若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
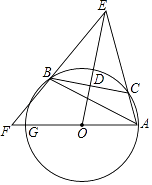
(1)点点同学通过画图和测量得到以下近似数据:ɑ
30°
40°
50°
60°
β
120°
130°
140°
150°
γ
150°
140°
130°
120°
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.若一组数据是1,2,3,4,5,则它的方差是3
B.若分式方程 有增根,则它的增根是1
有增根,则它的增根是1
C.对角线互相垂直的四边形,顺次连接它的四边中点所得四边形是矩形
D.若一个角的两边分别与另一个角的两边平行,则这两个角相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y=
 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1 , y1),M2(x2 , y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(2 ,﹣
,﹣  ).
).
其中正确的结论个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3
 ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=  CE;④S阴影=
CE;④S阴影=  .其中正确结论的序号是 .
.其中正确结论的序号是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:20170﹣|1﹣
 |+(
|+(  )﹣1+2cos45°.
)﹣1+2cos45°.
相关试题

