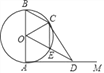
【题目】如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接OC、BC、CE.
(1)求证:CD是⊙O的切线;
(2)若圆O的直径等于2,填空:
①当AD= 时,四边形OADC是正方形;
②当AD= 时,四边形OECB是菱形.
参考答案:
【答案】(1)见解析;(2)①1;②![]() .
.
【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;
(2)①依据正方形的四条边都相等可知AD=OA;
②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.
试题解析:解:∵AM⊥AB,
∴∠OAD=90°.
∵OA=OC,OD=OD,AD=DC,
∴△OAD≌△OCD,
∴∠OCD=∠OAD=90°.
∴OC⊥CD,
∴CD是⊙O的切线.
(2)①∵当四边形OADC是正方形,
∴AO=AD=1.
故答案为:1.
②∵四边形OECB是菱形,
∴OE=CE.
又∵OC=OE,
∴OC=OE=CE.
∴∠CEO=60°.
∵CE∥AB,
∴∠AOD=60°.
在Rt△OAD中,∠AOD=60°,AO=1,
∴AD=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
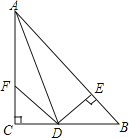
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,BC=8,AB=10,则△FCD的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(
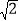 ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是平行四边形ABCD的边BC的中点,连接AE并延长交DC的延长线于点F,连接AC、BF,∠AEC=2∠ABC;(1)求证:四边形ABFC是矩形;(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积。

-
科目: 来源: 题型:
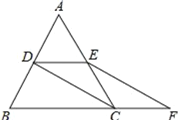
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
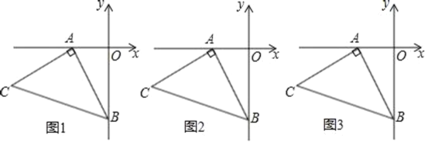
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:

(1)按第①行数排列的规律,第7个数是____,第
 个数是_______(用含
个数是_______(用含 的式子表示)
的式子表示)(2)观察第②行数与第①行数的关系,第②行第
 个数是________(用含
个数是________(用含 的式子表示)
的式子表示)观察第③行数与第①行数的关系,第③行第
 个数是__________(用含
个数是__________(用含 的式子表示)
的式子表示)(3)取每行数的第8个数,计算这三个数的和.
相关试题

