【题目】如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=﹣x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).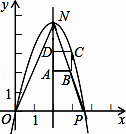
(参考公式:y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ![]() ,
, ![]() ).
).
(1)若当n=4时求c,b并写出抛物线对称轴及y的最大值;
(2)求证:抛物线的顶点在函数y=x2的图像上;
(3)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(4)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
参考答案:
【答案】
(1)
解:当n=4时,则P(4,0),
∵抛物线y=﹣x2+bx+c经过原点O和点P,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x=﹣(x﹣2)2+4,
∴抛物线对称轴为直线x=2,
∵﹣1<0,
∴当x=2时,y有最大值4
(2)
证明:把O、P的坐标代入抛物线解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+nx=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴抛物线顶点坐标为( ![]() ,
, ![]() ),
),
在y=x2中,当x= ![]() 时,y=
时,y= ![]() ,
,
∴抛物线的顶点在函数y=x2的图像上
(3)
解:在y=﹣x2+nx中,当x=2时,y=2n﹣4,
∴N点坐标为(2,2n﹣4),
∴N到x轴的距离为|2n﹣4|=2|n﹣2|,
∵P(n,0),
∴OP=n,
∴S△NPO= ![]() n×2|n﹣2|=n|n﹣2|,
n×2|n﹣2|=n|n﹣2|,
当△NPO的面积为1时,则有n|n﹣2|=1,
当n=2时,N、P重合,不成立,
当n>2时,则n2﹣2n=1,解得n=1+ ![]() 或n=1﹣
或n=1﹣ ![]() (此时n小于2,舍去),
(此时n小于2,舍去),
当0<n<2时,则2n﹣n2=1,解得n1=n2=1,
综上可知当n的值为1+ ![]() 或1时,△NPO的面积为1
或1时,△NPO的面积为1
(4)
解:∵抛物线解析式为y=﹣x2+nx,
∴当过A(2,2)时,代入可得2=﹣4+2n,解得n=3,
同理当抛物线过B时可求得n= ![]() ,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n=
,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n= ![]() ,
,
∴n的取值范围为3≤n≤4
【解析】(1)把原点和P点坐标代入抛物线解析式可求得b、c,则可求得抛物线解析式,化为顶点式可求得其对称轴和最大值;(2)用n可表示出抛物线的解析式,则可求得其顶点坐标,代入y=x2进行验证即可;(3)可用n表示出N点坐标,则可表示出N到x轴的距离和OP的长,可表示出△NPO的面积,可得到关于n的方程,可求得n的值;(4)分别把A、B、C、D的坐标代入抛物线解析式可求得n的值,则可求得n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平面直角坐标系xOy中,正比例函数y=
 x的图像经过点A,点A的纵坐标为6,反比例函数y=
x的图像经过点A,点A的纵坐标为6,反比例函数y=  的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: 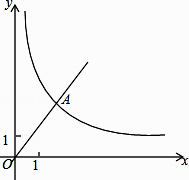
(1)这个反比例函数的解析式;
(2)直线AB(一次函数)的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.
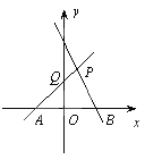
(1)求直线PA的表达式及Q点的坐标;
(2)求四边形PQOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
售价(元/本)
50
55
60
65
…
月销量(本)
2000
1800
1600
1400
…
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是元,②月销量是件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出
 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:
 填表:
填表:平均数(分)
中位数(分)
众数(分)
初中代表队


高中代表队


 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好; 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
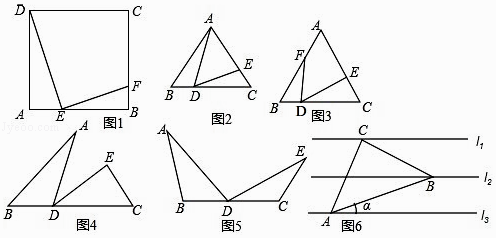
(1)如图1,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,证明:△ADE∽△BFE.
(2)这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”,那普通的3个等角又会怎样呢?
变式一如图2,已知等边三角形ABC,点D、E分别为BC,AC上的点,∠ADE=60°.
①图中有相似三角形吗?请说明理由.
②如图3,若将∠ADE在△ABC的内部(∠ADE两边不与BC重合),绕点D逆时针旋转一定的角度,还有相似三角形吗?
(3)变式二如图4,隐藏变式1图形中的线段AE,在得到的新图形中.
①如果∠B=∠C=∠ADE=50°,图中有相似三角形吗?请说明理由.
②如图5,若∠B=∠C=∠ADE=∠a,∠a为任意角,还有相似三角形吗?
(4)交式三已知,相邻两条平形直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则cosa的值是(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是马小哈同学做的一道题:
解方程:
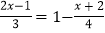
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得

(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:
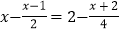 .
.
相关试题

