【题目】已知,如图,在平面直角坐标系xOy中,正比例函数y= ![]() x的图像经过点A,点A的纵坐标为6,反比例函数y=
x的图像经过点A,点A的纵坐标为6,反比例函数y= ![]() 的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
的图像也经过点A,第一象限内的点B在这个反比例函数的图像上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: 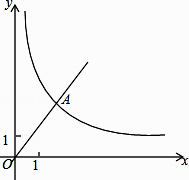
(1)这个反比例函数的解析式;
(2)直线AB(一次函数)的表达式.
参考答案:
【答案】
(1)解:∵正比例函数y= ![]() x的图像经过点A,点A的纵坐标为6,
x的图像经过点A,点A的纵坐标为6,
∴6= ![]() x,
x,
解得:x=4,
∴点A的坐标为(4,6),
∵反比例函数y= ![]() 的图像经过点A,
的图像经过点A,
∴m=6×4=24,
∴反比例函数的解析式为:y= ![]()
(2)解:如图,连接AC、AB,作AD⊥BC于D,
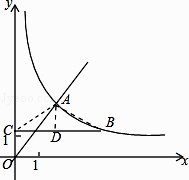
∵AC=AB,AD⊥BC,
∴BC=2CD=8,
∴点B的坐标为:(8,3),
设直线AB的表达式为:y=kx+b,
由题意得, ![]() ,
,
解得, 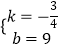 ,
,
∴直线AB的表达式为:y=﹣ ![]() x+9.
x+9.
【解析】(1)根据正比例函数y= ![]() x的图像经过点A,点A的纵坐标为4,求出点A的坐标,根据反比例函数y=
x的图像经过点A,点A的纵坐标为4,求出点A的坐标,根据反比例函数y= ![]() 的图像经过点A,求出m的值即可;(2)根据点A的坐标和等腰三角形的性质求出点B的坐标,运用待定系数法求出直线AB的表达式.
的图像经过点A,求出m的值即可;(2)根据点A的坐标和等腰三角形的性质求出点B的坐标,运用待定系数法求出直线AB的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过20立方米,每立方米按1.5元收费;如果超过20立方米,超过部分每立方米按1.8元收费,其余仍按每立方米1.5元计算,另外,超过的部分每立方米加收污水处理费1元,若某户一月份用水量
 (
(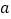 >20)立方米,问:
>20)立方米,问:(1)该户一月份应交水费多少元?(请用含
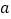 的代数式表示)
的代数式表示)(2)该户三月份用水量为32立方米,请问该户三月份应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
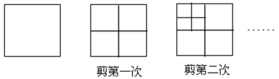
(1)完成下表:
剪的次数
1
2
3
4
5
...
n
小正方形的个数
4
7
10
...
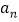
(2)
 .(用含n的代数式表示)
.(用含n的代数式表示)(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.
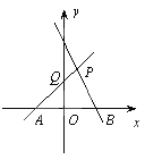
(1)求直线PA的表达式及Q点的坐标;
(2)求四边形PQOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
售价(元/本)
50
55
60
65
…
月销量(本)
2000
1800
1600
1400
…
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是元,②月销量是件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=﹣x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
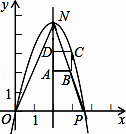
(参考公式:y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ,
, 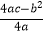 ).
).
(1)若当n=4时求c,b并写出抛物线对称轴及y的最大值;
(2)求证:抛物线的顶点在函数y=x2的图像上;
(3)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(4)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
相关试题

