【题目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当OB绕点O在
当OB绕点O在![]() 内旋转时,则
内旋转时,则![]() 的大小为______;
的大小为______;
![]() 如图2,若
如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 当
当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小;
的大小;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 内绕着点O以
内绕着点O以![]() 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时,![]() 和
和![]() 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值

参考答案:
【答案】(1)78°;(2)∠MON=66°;(3)当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.
【解析】
(1)由角平分线的定义可得∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON,即可求∠MON的大小;
∠BON,即可求∠MON的大小;
(2)由角平分线的定义可得∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,即可求∠MON的大小;
∠BOD,即可求∠MON的大小;
(3)由题意可得∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t,分∠AOM=2∠DON,∠DON=2∠AOM两种情况讨论,列出方程可求t的值.
(1)∵OM平分∠AOB,ON平分∠BOD,∴∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON.
∠BON.
∵∠MON=∠BOM+∠BON![]() ∠AOD,∴∠MON=78°.
∠AOD,∴∠MON=78°.
故答案为:78°.
(2)∵OM平分∠AOC,ON平分∠BOD,∴∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC
∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC![]() ∠AOC
∠AOC![]() ∠BOD﹣24°
∠BOD﹣24°![]() (∠AOC+∠BOD)﹣24°,∴∠MON
(∠AOC+∠BOD)﹣24°,∴∠MON![]() (∠AOD+∠BOC)﹣24°
(∠AOD+∠BOC)﹣24°![]() 180°﹣24°=66°.
180°﹣24°=66°.
(3)∵∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒,OM平分∠AOC,ON平分∠BOD,∴∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t.
若∠AOM=2∠DON时,即27+t=2(63﹣t),∴t=33;
若2∠AOM=∠DON,即2(27+t)=63﹣t,∴t=3.
综上所述:当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过200度的部分的电价为每度
 元.
元.第二档:月用电量超过200度但不超过400度部分的电价为每度
 元.
元.第三档:月用电量超过400度的部分的电价为每度
 元.
元. 已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元
已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元
 若去年6月份小明家用电的平均电价为
若去年6月份小明家用电的平均电价为 元,求小明家去年6月份的用电量.
元,求小明家去年6月份的用电量. 已知小明家去年7、8月份的用电量共700度
已知小明家去年7、8月份的用电量共700度 月份的用电量少于8月份的用电量
月份的用电量少于8月份的用电量 ,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
,两个月的总电价是384元,求小明家7、8月的用电量分别是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息知,乙到达A地的时刻为( )
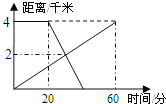
A. 8:30B. 8:35C. 8:40D. 8:45
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.

(1)已知BD= ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明. -
科目: 来源: 题型:
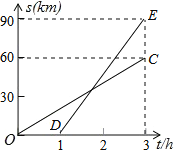
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及k值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB的平分线,OD是∠AOC的平分线,OE是∠BOD的平分线,且∠BOE=30°,求∠AOB的度数.

相关试题

