【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.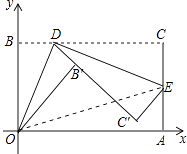
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
参考答案:
【答案】
(1)
解:由折叠的性质可知,∠ODB=∠ODB′,∠EDC=∠EDC′,
∴∠ODE=90°,
∴∠BDO+∠CDE=90°,又∠BDO+∠BOD=90°,
∴∠BOD=∠CDE,
∵BD=t=1,BC=4,
∴CD=3,又OB=3,
∴OB=CD,
在△BOD和△CDE中,
 ,
,
∴△BOD≌△CDE,
∴CE=BD=1,
∴AE=AC﹣CE=2,
∴点E的坐标为(4,2)
(2)
解:∵BD=t,
∴DC=BC﹣BD=4﹣t,
由(1)得,∠BOD=∠CDE,又∠B=∠C=90°,
∴△ODB∽△DCE,
∴ ![]() ,即
,即 ![]() ,
,
解得,CE= ![]() t2+
t2+ ![]() t,
t,
∴S= ![]() ×(CE+OB)×BC=
×(CE+OB)×BC= ![]() ×(
×( ![]() t2+
t2+ ![]() t+3)×4,
t+3)×4,
∴S= ![]() t2+
t2+ ![]() t+6(0<t<4)
t+6(0<t<4)
(3)
解:在Rt△OEA中,OE2=OA2+AE2=42+AE2,
∴当AE最小时,OE最小,
由(2)得,CE= ![]() t2+
t2+ ![]() t,
t,
∴AE=AC﹣CE= ![]() t2﹣
t2﹣ ![]() t+3=
t+3= ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,
,
当t=2时,AE的最小值为 ![]() ,
,
此时点E的坐标为(4, ![]() )
)
【解析】(1)根据折叠的性质和全等三角形的判定定理证明△BOD≌△CDE,求出CE,计算出AE,得到点E的坐标;(2)根据相似三角形的性质用t表示出CE,根据梯形的面积公式用t表示S;(3)根据二次函数的性质求出AE的最小值,求出点E的坐标.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.

(1)求证:CE是半圆的切线;
(2)若OB=5,BC=8,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )

A.②④
B.①④
C.②③
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则
 的值是( )
的值是( ) 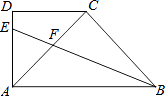
A.
B.
C. +1
+1
D.
相关试题

