【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
参考答案:
【答案】
(1)解:y=ax2﹣2x=a(x﹣ ![]() )2﹣
)2﹣ ![]() ,则B的坐标是(
,则B的坐标是( ![]() ,﹣
,﹣ ![]() )
)
(2)解:∵点C的坐标是(0,﹣2),
∴OC=2,
设抛物线的对称轴与x轴相交于点F.
∵EF∥y轴,F是OA的中点,
∴EF= ![]() CO=1.
CO=1.
∵△OCD≌△BED,
∴BE=CO=2,
∴BF=BE+EF=3.
∴﹣ ![]() =﹣3,
=﹣3,
∴a= ![]() .
.
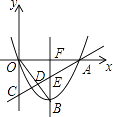
【解析】(1)利用配方法即可求得B的坐标;(2)依据△OCD≌△BED可得BE=CO,据此即可求得BF的长,根据B的坐标求得a的值.
【考点精析】利用抛物线与坐标轴的交点和全等三角形的性质对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,BD是对角线.

(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆的直径,点C是弧AD的中点,过点C作BD延长线的垂线交于点E.

(1)求证:CE是半圆的切线;
(2)若OB=5,BC=8,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
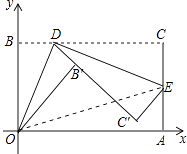
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
相关试题

