【题目】如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则 ![]() 的值是( )
的值是( ) 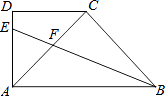
A.![]()
B.![]()
C.![]() +1
+1
D.![]()
参考答案:
【答案】C
【解析】解:作FG⊥AB于点G, 
∵∠DAB=90°,
∴AE∥FG,
∴ ![]() =
= ![]() ,
,
∵AC⊥BC,
∴∠ACB=90°,
又∵BE是∠ABC的平分线,
∴FG=FC,
在Rt△BGF和Rt△BCF中,![]()
∴Rt△BGF≌Rt△BCF(HL),
∴CB=GB,
∵AC=BC,
∴∠CBA=45°,
∴AB= ![]() BC,
BC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() +1.
+1.
故选:C.
作FG⊥AB于点G,由AE∥FG,得出 ![]() =
= ![]() ,求出Rt△BGF≌Rt△BCF,再由AB=
,求出Rt△BGF≌Rt△BCF,再由AB= ![]() BC求解.
BC求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
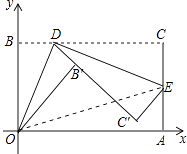
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )

A.②④
B.①④
C.②③
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=
 (x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积= .
(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共吨;
(3)调查发现,在可回收物中塑料类垃圾占 ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5m-7n-8p+5n-9m-p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5.
【答案】(1)-4m-2n-9p;(2)3x16
【解析】
(1)先移项,再合并同类项;
(2)原式利用幂的乘方、同底数幂的乘法和除法法则计算,再合并即可得到结果.
(1)5m-7n-8p+5n-9m-p=5m-9m-7n+5n-8p-p=-4m-2n-9p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5=- x4x5x7+5x16-x21÷x5=- x16 +5x16-x16=3x16
【点睛】
此题考查了幂的乘方、同底数幂的乘法、除法法则计算以及合并同类项,熟练掌握整式运算的有关法则是解答此题的关键.
【题型】解答题
【结束】
21【题目】解方程:
 (x-2)-
(x-2)- (4x-1)=4.
(4x-1)=4.
相关试题

