Question

【题目】如图，过点B，D分别向线段AE作垂线段BQ和DF，点Q和F是垂足，连结AB，DE，BD，BD交AE于点C，且AB＝DE，AF＝EQ．

(1)求证：△ABQ≌△EDF；

(2)求证：C是BD的中点．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据AF＝EQ推出AQ＝EF，则可证明△ABQ≌△EDF(HL)；

（2）由（1）得BQ＝FD，则根据垂直与对顶角，即可证明△BQC≌△DFC(AAS)，即可推出C是BD的中点．

解： (1)∵AF＝EQ，∴AQ＝EF，

在Rt△ABQ与Rt△EDF中，

∴△ABQ≌△EDF(HL)．

(2)∵△ABQ≌△EDF，

∴BQ＝FD，

在△BQC与△DFC中，

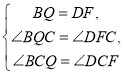
∴△BQC≌△DFC(AAS)，

∴BC＝CD

∴C是BD的中点．