【题目】已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论:
①关于x的一元二次方程ax2+bx+c=0的根是﹣1,3;②abc>0;③a+b=c﹣b;④y最大值=![]() c;⑤a+4b=3c中正确的有_____(填写正确的序号)
c;⑤a+4b=3c中正确的有_____(填写正确的序号)

参考答案:
【答案】①③④
【解析】
由抛物线与x轴的一个交点坐标及对称轴为x=1,利用对称性得到另一个交点的坐标,可得出ax2+bx+c=0的两个解为-1,3,选项①正确;由抛物线开口向下得到a小于0,对称轴在y轴右侧,得到b大于0,与y轴交点在正半轴得到c大于0,进而得到abc小于0,选项②错误; ③由对称轴是:x=1=﹣![]() ,得b=﹣2a,所以,a+b=﹣a,由抛物线与x轴另一个交点为(﹣1,0),得a﹣b+c=0,所以,a+b=c﹣b,选项③正确;
,得b=﹣2a,所以,a+b=﹣a,由抛物线与x轴另一个交点为(﹣1,0),得a﹣b+c=0,所以,a+b=c﹣b,选项③正确;
④由a﹣b+c=0和b=﹣2a得:a=﹣![]() c,所以,y最大值=
c,所以,y最大值=![]() =
=![]() ,选项④正确;
,选项④正确;
⑤a+4b=﹣7a=﹣7×![]() =
=![]() ,选项⑤错误;
,选项⑤错误;
①∵抛物线与x轴一个交点为(3,0),且对称轴为x=1,
∴抛物线与x轴另一个交点为(﹣1,0),
即关于x的一元二次方程ax2+bx+c=0的解为﹣1,3,
选项①正确;
②∵二次函数图象开口向下,对称轴在y轴右侧,与y轴交点在正半轴,
∴ab<0,c>0,即abc<0,
选项②错误;
③由对称轴是:x=1=﹣![]() ,得b=﹣2a,
,得b=﹣2a,
∴a+b=a﹣2a=﹣a,
∵抛物线与x轴另一个交点为(﹣1,0),
∴a﹣b+c=0,
∴c﹣b=﹣a,
∴a+b=c﹣b,
选项③正确;
④由a﹣b+c=0和b=﹣2a得:a=﹣![]() c,
c,
∴y最大值=![]() =c﹣
=c﹣![]() =c﹣
=c﹣![]() =c﹣(﹣
=c﹣(﹣![]() c)=
c)=![]() ,
,
选项④正确;
⑤∵a+4b=a﹣8a=﹣7a=﹣7×![]() =
=![]() ,
,
选项⑤错误;
综上所述,本题正确的结论有:①③④;
故答案为:①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点B,D分别向线段AE作垂线段BQ和DF,点Q和F是垂足,连结AB,DE,BD,BD交AE于点C,且AB=DE,AF=EQ.

(1)求证:△ABQ≌△EDF;
(2)求证:C是BD的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
-
科目: 来源: 题型:
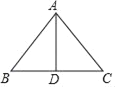
查看答案和解析>>【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2
 ,AE=8,则ED=______.
,AE=8,则ED=______.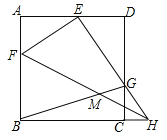
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣ )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
相关试题

