【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

参考答案:
【答案】2
【解析】
过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.
过P作PE⊥OB,交OB与点E,
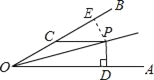
∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE=![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若将f(x)的图象向左平移
,若将f(x)的图象向左平移  个单位后所得函数的图象关于原点对称,则φ=( )
个单位后所得函数的图象关于原点对称,则φ=( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足
内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足 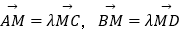 (其中λ>0,且λ≠1),若λ变化时,AB的斜率总为
(其中λ>0,且λ≠1),若λ变化时,AB的斜率总为  ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=5,在AC上取一E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )

A. 1 B.
 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且
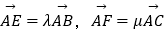 ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 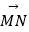 的最小值为 .
的最小值为 . 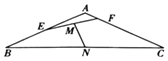
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是等边三角形,在BC边上取点D,在边AC的延长线上取点E使DE=AD.
求证:BD=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为,且满足
 .
.
(1)求角A的大小;
(2)若D为BC上一点,且 ,求a.
,求a.
相关试题

