【题目】已知:如图,△ABC是等边三角形,在BC边上取点D,在边AC的延长线上取点E使DE=AD.
求证:BD=CE.

参考答案:
【答案】证明见解析.
【解析】
由题意,不难得出∠ADC>60°,即∠ADB<∠DCE=120°;因此可以通过证△ABD和△DEC全等来得出结论.因此要构建全等三角形,过D作DF∥AE交AB于F,则△BDF是等边三角形,即BD=DF,因此只需证明△ADF≌△DEC即可.
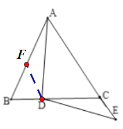
证明:作DF∥AE交AB于F,
∴△ABC是正三角形,可得△FBD是正三角形
∴FB=DB=DF,AB-FB=BC-DB,AF=DC
∵DA=DE,∴∠DAE=∠E,∠FAD=∠CDE
在△AED和△DCE中

∴△AFD≌△DCE(SAS)
∴DF=CE,即BD=CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=5,在AC上取一E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )

A. 1 B.
 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且
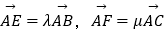 ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 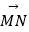 的最小值为 .
的最小值为 . 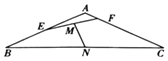
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为,且满足
 .
.
(1)求角A的大小;
(2)若D为BC上一点,且 ,求a.
,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.

(1)求证:AE∥平面PCD;
(2)记平面PAB与平面PCD的交线为l,求二面角C﹣l﹣B的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制.

(Ⅰ)地产数据研究院研究发现,3月至7月的各月均价y(万元/平方米)与月份x之间具有较强的线性相关关系,试建立y关于x的回归方程(系数精确到0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(Ⅱ)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
参考数据: =25,
=25,  =5.36,
=5.36,  =0.64
=0.64
回归方程 =
=  x+
x+  中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: =
=  ,
,  =
=  ﹣
﹣  .
.
相关试题

