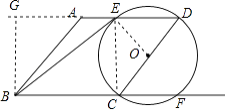
【题目】如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F, 
(1)若cos∠AEB= ![]() ,则菱形ABCD的面积为;
,则菱形ABCD的面积为;
(2)当BE与⊙O相切时,AE的长为 .
参考答案:
【答案】
(1)8 ![]()
(2)6﹣2 ![]()
【解析】解:(1.)作BG⊥AD于G,连接CE,
∵四边形ABCD是菱形∴AB=AD=BC=CD=4,AD∥BC,∵CD是直径,∴∠CED=90°,∴CE⊥AD,∴BG∥CE,∴四边形BCEG是矩形,∴GE=BC=4,∵cos∠AEB= ![]() ,∴
,∴ ![]() =
= ![]() ,∴BE=
,∴BE= ![]() ×4=6,∴BG=
×4=6,∴BG= ![]() =
= ![]() =2
=2 ![]() ,∴菱形ABCD的面积=ADBG=4×2
,∴菱形ABCD的面积=ADBG=4×2 ![]() =8
=8 ![]() ;
;
所以答案是8 ![]() ;
;
(2.)连接OE,∵BE与⊙O相切,∴FE⊥BE,∴∠BEG=∠CEO,∵OE=OC,∴∠DCE=∠CEO,∴∠ECD=∠GEB,∴ ![]() =
= ![]() ,∵GE=AD,∴AG=ED,设BG=CE=a,∴
,∵GE=AD,∴AG=ED,设BG=CE=a,∴ ![]() =
= ![]() ,∴16﹣a2=4AE,∴AG2=4AE,即(4﹣AE)2=4AE,∴AE2﹣12AE+16=0,解得AE=6﹣2
,∴16﹣a2=4AE,∴AG2=4AE,即(4﹣AE)2=4AE,∴AE2﹣12AE+16=0,解得AE=6﹣2 ![]() 或AE=6+2
或AE=6+2 ![]() (不合题意,舍去),所以答案是6﹣2
(不合题意,舍去),所以答案是6﹣2 ![]() .
.
【考点精析】利用菱形的性质和切线的性质定理对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=kx与抛物线y=
 交于点A(3,6).
交于点A(3,6).
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆货车分别从
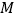 、
、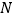 两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知
两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知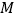 、
、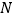 两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程
两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程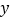 (千米)与甲车出发时间
(千米)与甲车出发时间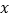 (分钟)的函数图像如图所示.
(分钟)的函数图像如图所示.(1)甲车从
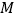 地出发后,经过多长时间甲、乙两车第一次相遇?
地出发后,经过多长时间甲、乙两车第一次相遇?(2)乙车从
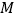 地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?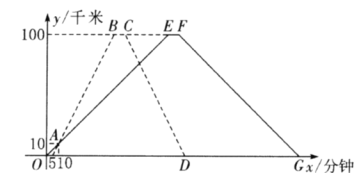
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.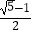
B.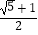
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB
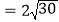 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )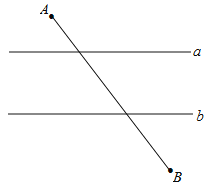
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
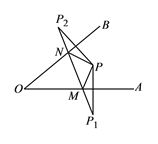
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )

A. 140° B. 120° C. 130° D. 无法确定
相关试题

