【题目】甲、乙两辆货车分别从![]() 、
、![]() 两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知
两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知![]() 、
、![]() 两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程
两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程![]() (千米)与甲车出发时间
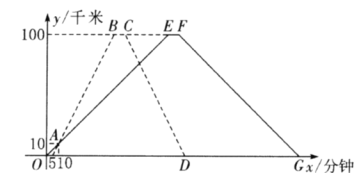
(千米)与甲车出发时间![]() (分钟)的函数图像如图所示.
(分钟)的函数图像如图所示.
(1)甲车从![]() 地出发后,经过多长时间甲、乙两车第一次相遇?
地出发后,经过多长时间甲、乙两车第一次相遇?
(2)乙车从![]() 地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
参考答案:
【答案】(1)甲车从![]() 地出发后,经过
地出发后,经过![]() 分钟,甲、乙两车第一次相遇。 (2)乙车从
分钟,甲、乙两车第一次相遇。 (2)乙车从![]() 地出发后,经过
地出发后,经过![]() 分钟,甲、乙两车与各自出发地的距离相等.
分钟,甲、乙两车与各自出发地的距离相等.
【解析】
(1)直接利用待定系数法求解得出直线AB的解析式y=2x-10,线OE的解析式为y=x,联立方程组求交点坐标即可;
(2)根据题意求出直线CD的解析式为y=-2x+220,与y=x联立方程组求解,x=y=![]() ,可得
,可得 ![]() 分钟.
分钟.
(1)设直线AB的解析式为y=k1x+b1 ,
∴将(5,0)和(10,10)代入得:![]() ,
,
解得:![]() ,
,
∴直线AB解析式为y=2x10.
设直线OE的解析式为y=k2x,将(10,10)代入得:10k2=10,
∴k2=1,
即直线OE的解析式为y=x,
当两车第一次相遇时,(2x10)+x=100,
∴x=![]() .
.
答:甲车从M地出发后,经过![]() 分钟甲、乙两车第一次相遇;
分钟甲、乙两车第一次相遇;
(2)由题意得100=2xB10
∴xB=55
∴xC=xB+5=60
由题可知xDxC=xB5
即xD=110,
设直线CD的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线CD的解析式为y=2x+220
∴![]() ,
,
∴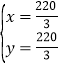 ,
,
∴![]() .
.
答:乙车从M地出发后,又经过403分钟,甲、乙两车与各自出发地的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平安加气站某日8:00的储气量为10 000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量
 (立方米)与时间
(立方米)与时间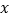 (小时)之间的函数关系如图中的折线
(小时)之间的函数关系如图中的折线 所示.
所示.(1)分别求出8:00 ~8:30及8:30之后加气站的储气量
 (立方米)与时间
(立方米)与时间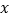 (小时)之间的函数表达式.
(小时)之间的函数表达式.(2)前30辆车能否在当天8:42之前加完气?
(3)若前
 辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求
辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=kx与抛物线y=
 交于点A(3,6).
交于点A(3,6).
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个? -
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.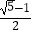
B.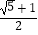
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F,

(1)若cos∠AEB= ,则菱形ABCD的面积为;
,则菱形ABCD的面积为;
(2)当BE与⊙O相切时,AE的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB
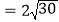 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )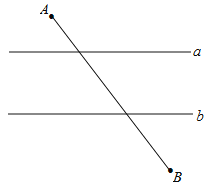
A. 6 B. 8 C. 10 D. 12
相关试题

