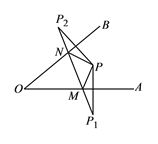
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
参考答案:
【答案】15 96°
【解析】
P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N.由此即可得到△PMN的周长.根据四边形内角和为360°,可得出∠P1PP2的度数,根据等腰三角形的性质和三角形外角的性质可得出∠PNM+∠PMN的度数,再根据三角形内角和定理即可得出∠MPN的度数.
∵P点关于OA的对称是点P1,P点关于OB的对称点P2,∴PM=P1M,PN=P2N,PP2⊥OB,PP1⊥OA,∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15,∠P1PP2=360°-90°-90°-42°=138°,∠P2=∠NPP2,∠P1=∠P1PM,∴∠PNM=2∠P2,∠PMN=2∠P1,∴∠PNM+∠PMN=2∠P1+2∠P2=2(180°-∠P1PP2)=84°,∴∠MPN=180°-(∠PNM+∠PMN)=180°-84°=96°.
故答案为:15,96°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.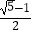
B.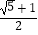
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F,

(1)若cos∠AEB= ,则菱形ABCD的面积为;
,则菱形ABCD的面积为;
(2)当BE与⊙O相切时,AE的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB
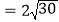 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )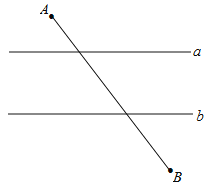
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )

A. 140° B. 120° C. 130° D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )

A. 120° B. 125° C. 130° D. 155°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
相关试题

