【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
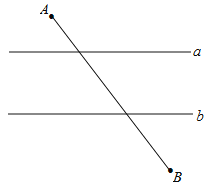
A. 6 B. 8 C. 10 D. 12
参考答案:
【答案】B
【解析】
MN表示直线a与直线b之间的距离,是定值,只要满足AM+NB的值最小即可.过A作直线a的垂线,并在此垂线上取点A′,使得AA′=MN,连接A'B,则A'B与直线b的交点即为N,过N作MN⊥a于点M.则A'B为所求,利用勾股定理可求得其值.
过A作直线a的垂线,并在此垂线上取点A′,使得AA′=4,连接A′B,与直线b交于点N,过N作直线a的垂线,交直线a于点M,连接AM,过点B作BE⊥AA′,交射线AA′于点E,如图,∵AA′⊥a,MN⊥a,∴AA′∥MN.
又∵AA′=MN=4,∴四边形AA′NM是平行四边形,∴AM=A′N.
由于AM+MN+NB要最小,且MN固定为4,所以AM+NB最小.
由两点之间线段最短,可知AM+NB的最小值为A′B.
∵AE=2+3+4=9,AB![]() ,∴BE
,∴BE![]() .
.
∵A′E=AE﹣AA′=9﹣4=5,∴A′B![]() 8.
8.
所以AM+NB的最小值为8.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆货车分别从
 、
、 两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知
两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知 、
、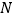 两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程
两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程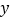 (千米)与甲车出发时间
(千米)与甲车出发时间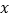 (分钟)的函数图像如图所示.
(分钟)的函数图像如图所示.(1)甲车从
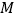 地出发后,经过多长时间甲、乙两车第一次相遇?
地出发后,经过多长时间甲、乙两车第一次相遇?(2)乙车从
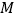 地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?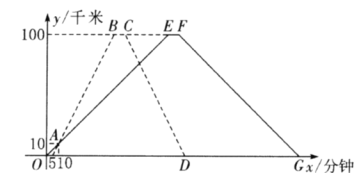
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.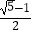
B.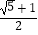
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F,

(1)若cos∠AEB= ,则菱形ABCD的面积为;
,则菱形ABCD的面积为;
(2)当BE与⊙O相切时,AE的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
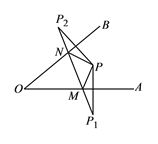
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )

A. 140° B. 120° C. 130° D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )

A. 120° B. 125° C. 130° D. 155°
相关试题

