【题目】综合与实践
如图1,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .我们可以发现:反比例函数
.我们可以发现:反比例函数![]() 的图象是一个关于原点中心对称的图形.
的图象是一个关于原点中心对称的图形.
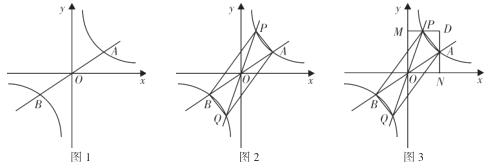
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)利用所给函数图象,写出不等式![]() 的解集 ;
的解集 ;
(3)如图2,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .试说明以
.试说明以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,但不可能是正方形;
为顶点的四边形一定是平行四边形,但不可能是正方形;
(4)如图3,当点![]() 在点
在点![]() 的左上方时,过
的左上方时,过![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线轴于点
![]() ,交直线
,交直线![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() .求点
.求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析;(4)点
;(3)见解析;(4)点![]() 的坐标为
的坐标为![]()
【解析】
(1)由题意直接把点A(3,2)代入一次函数及反比例函数的解析式求出k1及a的值,再根据反比例函数的图象关于原点对称可得出m、n的值;
(2)由题意直接根据两函数的图象即可得出结论;
(3)根据题意利用“反比例函数的图象是一个关于原点中心对称的图形”得:OA=OB,OP=OQ,故以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,并由
为顶点的四边形一定是平行四边形,并由![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,即可得出以
不可能互相垂直,即可得出以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形;
为顶点的四边形不可能是菱形,也就不可能是正方形;
(4)根据题意设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形,故可得出OM×PM=6,ON×AN=6,根据
是矩形,故可得出OM×PM=6,ON×AN=6,根据![]() 可得出其面积,
可得出其面积,![]() 可求出ONOM的值,由此可得出结论.
可求出ONOM的值,由此可得出结论.
解:(1)∵正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(3,2),
的图象交于点A(3,2),
∴![]() ,解得
,解得![]() ,解得a=6.
,解得a=6.
∵正比例函数与反比例函数的图象均关于原点对称,
∴B(-3,-2),
∴m=-3,n=-2.
故答案为:![]() ;
;![]() ;
;![]() ;
;![]() .
.
(2)∵A(3,2)、B(-3,-2),
∴当x<-3或0<x<3时,![]() .
.
故答案为:x<-3或0<x<3.
(3)∵反比例函数的图象是一个关于原点中心对称的图形,
∴![]() ,
,![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形.
为顶点的四边形一定是平行四边形.
∵点![]() 、
、![]() 都在第一象限,
都在第一象限,
∴![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,
不可能互相垂直,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形.
为顶点的四边形不可能是菱形,也就不可能是正方形.
(4)设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形.
是矩形.
∵![]() 和
和![]() 都在双曲线上,
都在双曲线上,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图是一个正方形纸片
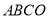 ,如果将正方形纸片
,如果将正方形纸片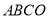 绕点
绕点 逆时针旋转角度
逆时针旋转角度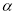
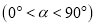 ,得到正方形
,得到正方形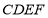 ,
,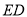 交
交 于点
于点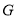 ,
,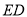 的延长线交
的延长线交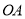 于点
于点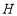 ,连接
,连接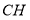 、
、 .
.
(1)求证:
 平分
平分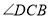 ;
;(2)直接写出线段
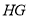 、
、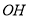 、
、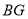 之间的数量关系;
之间的数量关系;(3)连接
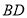 ,
,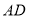 ,
, ,
,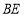 ,试探究在旋转过程中,四边形
,试探究在旋转过程中,四边形 能否成为矩形?请说明理由.
能否成为矩形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】新知探究: 光在反射时,光束的路径可用图(1)来表示.
 叫做入射光线,
叫做入射光线, 叫做反射光线,从入射点
叫做反射光线,从入射点 引出的一条垂直于镜面
引出的一条垂直于镜面 的射线
的射线 叫做法线.
叫做法线.  与
与 的夹角
的夹角 叫入射角,
叫入射角, 与
与 的夹角
的夹角 叫反射角.根据科学实验可得:
叫反射角.根据科学实验可得: .则图(1)中
.则图(1)中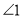 与
与 的数量关系是: 理由: ;
的数量关系是: 理由: ;问题解决: 生活中我们可以运用“激光”和两块相交的平面镜进行测距.如图(2)当一束“激光”
 射入到平面镜
射入到平面镜 上、被
上、被 反射到平面镜
反射到平面镜 上,又被平面镜
上,又被平面镜 反射后得到反射光线
反射后得到反射光线 .
.(1)若反射光线
 沿着入射光线
沿着入射光线 的方向反射回去,即
的方向反射回去,即 ,且
,且 ,则
,则
, 
 ;
;(2)猜想:当

 时,任何射到平面镜
时,任何射到平面镜 上的光线
上的光线 经过平面镜
经过平面镜 和
和 的两次反射后,入射光线
的两次反射后,入射光线 与反射光线
与反射光线 总是平行的.请你根据所学过的知识及新知说明.
总是平行的.请你根据所学过的知识及新知说明.
-
科目: 来源: 题型:
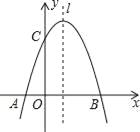
查看答案和解析>>【题目】如图,已知抛物线y=
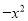 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
-
科目: 来源: 题型:
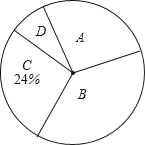
查看答案和解析>>【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节省空间,家里的饭碗一般是竖直摆放的,如果
 只饭碗(形状、大小相同)竖直摆放的高度为
只饭碗(形状、大小相同)竖直摆放的高度为 只饭碗竖直摆放的高度为
只饭碗竖直摆放的高度为 .如图所示,小颖家的碗橱每格的高度为
.如图所示,小颖家的碗橱每格的高度为 则一摞碗竖直放人橱柜时,每格最多能放________________________.
则一摞碗竖直放人橱柜时,每格最多能放________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图与图形变换
(尺规作图)(不写作法,保留作图痕迹)
如图,一辆汽车在直线形的公路上由点A向点B行驶,M,N 是分别位于公路两侧的村庄.
(1)在图1中求作一点P,使汽车行驶到此位置时,与村庄M,N的距离之和最小;

(2)在图2中求作一点Q,使汽车行驶到此位置时,与村庄 M,N 的距离相等.

(图形变换)
如图3所示,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(3)把△ABC 沿 BA 方向平移后,点 A 移到点
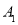 ,请你在网格中画出平移后得到的
,请你在网格中画出平移后得到的 ;
;(4)把
 绕点
绕点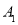 按逆时针方向旋转 90°,请你在网格中画出旋转后的
按逆时针方向旋转 90°,请你在网格中画出旋转后的 .
.
相关试题

