【题目】已知二次函数y=(x+m)2﹣n的图象如图所示,则一次函数y=mx+n与反比例函数y= ![]() 的图象可能是( )
的图象可能是( )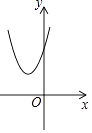
A.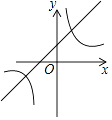
B.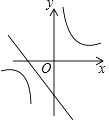
C.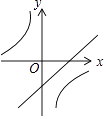
D.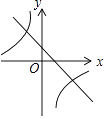
参考答案:
【答案】C
【解析】解:观察二次函数图象可知:m>0,n<0,
∴一次函数y=mx+n的图象经过第一、三、四象限,反比例函数y= ![]() 的图象在第二、四象限.
的图象在第二、四象限.
所以答案是:C.
【考点精析】利用一次函数的图象和性质和反比例函数的图象对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为
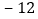 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒. 当
当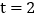 时,
时,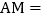 ______个单位长度,
______个单位长度,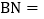 ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;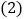 在运动过程中,当
在运动过程中,当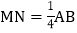 时,求点M所对应的有理数.
时,求点M所对应的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
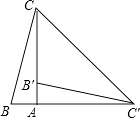
A.32°
B.64°
C.77°
D.87° -
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为
 千克时,运费为
千克时,运费为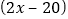 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为 千克时,运费为
千克时,运费为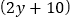 元。
元。(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).

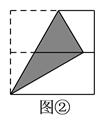


A.
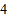 个 B.
个 B. 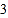 个 C.
个 C. 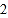 个 D.
个 D. 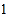 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
相关试题

