【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
参考答案:
【答案】(1)6元;(2)26千克;(3)首件物品的重量为10千克,第二件物品的重量为25千克.
【解析】
(1)根据新客户所寄首件物品的重量为x千克(x>10)时,运费为(2x-20)元,把x=13代入2x-20,计算即可求解;
(2)根据快递公司针对新客户首件物品的收费标准,可知2x-20=32,解方程即可求解;
(3)设首件物品的重量为2a千克,则第二件物品的重量为5a千克,分①0<2a≤10;②2a>10两种情况进行讨论.
解:(1)∵13>10,
∴运费为:2×13-20=6(元).
答:若新客户所寄首件物品的重量为13千克,则运费是6元;
(2)由题意,得2x-20=32,
解得x=26.
答:若新客户所寄首件物品的运费为32元,则物品的重量是26千克;
(3)设首件物品的重量为2a千克,则第二件物品的重量为5a千克.
①当0<2a≤10,即0<a≤5时,
2×5a+10=60,解得a=5,
此时2a=10,5a=25;
②当2a>10,即a>5时,
2×2a-20+2×5a+10=60,解得a=5,
a不大于5,
∴此情况不符合题意,舍去.
综上,首件物品的重量为10千克,第二件物品的重量为25千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达到每毫升6微克,接着就逐步衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量
 (微克)随时间
(微克)随时间 (小时)的变化如图所示,那么成年人规定剂量服药后:
(小时)的变化如图所示,那么成年人规定剂量服药后: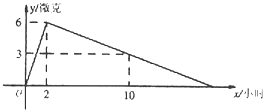
(1)y与x之间的函数关系式.
(2)如果每毫升血液中含药量在4微克或4微克以上时,治疗疾病才是有效的,那么这个有效时
间是多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y-4与x成正比,当x=1时,y=2
(1)求y与x之间的函数关系式,在下列坐标系中画出函数图象;
(2)当x=
 时,求函数y的值;
时,求函数y的值;(3)结合图象和函数的增减性,求当y<-2时自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
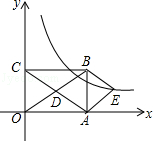
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波轨道交通4号线已开工建设,计划2020年通车试运营.为了了解镇民对4号线地铁票的定价意向,某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查,并将调查结果整理后制成了如下统计图,根据图中所给出的信息解答下列问题:
(1)求本次调查中该兴趣小组随机调查的人数;
(2)请你把条形统计图补充完整;
(3)如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是
(4)假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?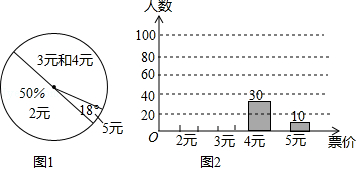
相关试题

