【题目】如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD. 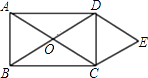
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为8 ![]() ,求AC的长.
,求AC的长.
参考答案:
【答案】
(1)证明:∵DE∥OC,CE∥OD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴四边形OCED是菱形
(2)解:∵∠ACB=30°,
∴∠DCO=90°﹣30°=60°.
又∵OD=OC,
∴△OCD是等边三角形.
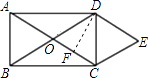
过D作DF⊥OC于F,则CF= ![]() OC,设CF=x,则OC=2x,AC=4x.
OC,设CF=x,则OC=2x,AC=4x.
在Rt△DFC中,tan60°= ![]() ,
,
∴DF= ![]() x.
x.
∴OCDF=8 ![]() .
.
∴x=2.
∴AC=4×2=8.
【解析】(1)熟记菱形的判定定理,本题可用一组邻边相等的平行四边形是菱形.(2)因为∠ACB=30°可证明菱形的一条对角线和边长相等,可证明和对角线构成等边三角形,然后作辅助线,根据菱形的面积已知可求解.
【考点精析】根据题目的已知条件,利用矩形的性质和解直角三角形的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式
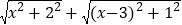 的最小值.
的最小值.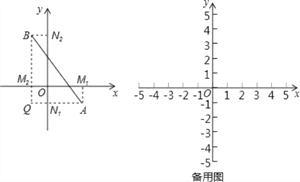
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包种植某水果,今年投资30 000元,收获水果20 000千克.此水果在市场上的售价为每千克
 元,卖给到果园收购的商贩每千克
元,卖给到果园收购的商贩每千克 元(
元( .若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
.若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.(1)分别用含
 的代数式表示两种出售方式的纯收入.
的代数式表示两种出售方式的纯收入.(2)若
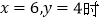 ,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.(3)该农户总结今年的种植及销售的经验,加强果园管理,力争明年纯收入达到100000元,则与(2)中今年较好的出售方式的纯收入相比,明年的纯收入的增长率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中菲黄岩岛争端持续,我海监船加大黄岩岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,黄岩岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向黄岩岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出C处的位置;

(2)求我国海监船行驶的航程BC的长.
-
科目: 来源: 题型:
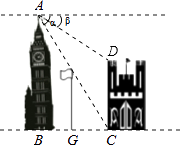
查看答案和解析>>【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用“”表示一种新运算符号,观察下列式子,解决问题:
25=2×2+4=8
34=2×3+3=9
3(﹣1)=2×3﹣2=4
﹣3(﹣5)=2×(﹣3)﹣6=﹣12
……
(1)请你用含a,b的式子表示这个规律:求ab的值;
(2)求(﹣
 6)(﹣4)的值;
6)(﹣4)的值;(3)如果x(﹣3)=3x,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
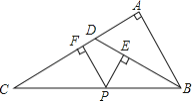
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

