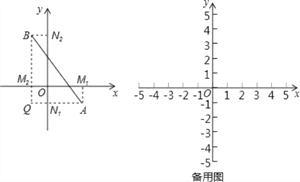
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() ;(2)5;(3)
;(2)5;(3)
【解析】分析:(1)通过作铅垂线构造直角三角形,利用勾股定理进行求解即可,
(2)根据(1)结论代入两点坐标计算即可,(3) 代数式![]() +
+![]() 的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,可以通过作对称转化为两点间线段距离最短,再利用两点之间距离公式计算即可求解.
的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,可以通过作对称转化为两点间线段距离最短,再利用两点之间距离公式计算即可求解.
详解:(1)∵AB2=AQ2+BQ2=|x1﹣x2|2+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,
∴AB=![]() ,故答案为
,故答案为![]() .
.
(2)∵A(1,﹣3),B(﹣2,1),
∴AB=![]() =5,故答案为5.
=5,故答案为5.
(3)代数式![]() +
+![]() 的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,如图,
的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小,如图,
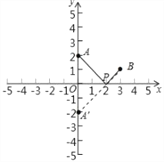
作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,
∵A′(0,﹣2),B(3,1),
∴PA+PB=PA′+PB=BA′=![]() =3
=3![]()
∴代数式![]() +
+![]() 的最小值为3
的最小值为3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
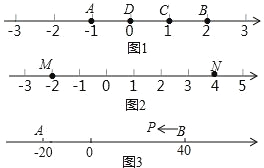
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,那么抽中20元奖品的概率为 .
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少? -
科目: 来源: 题型:
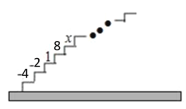
查看答案和解析>>【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣4,﹣2,1,8,且任意相邻四个台阶上数的和都相等.
尝试:(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用: 求从下到上39个台阶上数的和.
发现:试用含k(k为正整数)的代数式表示出数“1”所在的台阶数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包种植某水果,今年投资30 000元,收获水果20 000千克.此水果在市场上的售价为每千克
 元,卖给到果园收购的商贩每千克
元,卖给到果园收购的商贩每千克 元(
元( .若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
.若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.(1)分别用含
 的代数式表示两种出售方式的纯收入.
的代数式表示两种出售方式的纯收入.(2)若
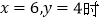 ,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.(3)该农户总结今年的种植及销售的经验,加强果园管理,力争明年纯收入达到100000元,则与(2)中今年较好的出售方式的纯收入相比,明年的纯收入的增长率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中菲黄岩岛争端持续,我海监船加大黄岩岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,黄岩岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向黄岩岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
(1)请用直尺和圆规作出C处的位置;

(2)求我国海监船行驶的航程BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
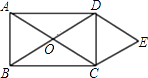
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为8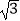 ,求AC的长.
,求AC的长.
相关试题

