【题目】若实数![]() 可以表示成两个连续自然数的倒数差,例如,
可以表示成两个连续自然数的倒数差,例如,![]() ,所以
,所以![]() 是第1个“l阶倒差数”倒差数”,
是第1个“l阶倒差数”倒差数”,![]() ,所以
,所以![]() 是第2个“l阶倒差数”,
是第2个“l阶倒差数”,![]() ,所以
,所以![]() 是第3个“l阶倒差数”……,即
是第3个“l阶倒差数”……,即![]() ,那么我们称
,那么我们称![]() 是第
是第![]() 个“l阶倒差数”;同理,
个“l阶倒差数”;同理,![]() 那么我们称
那么我们称![]() 为第
为第![]() 个“2阶倒差数”。
个“2阶倒差数”。
(l)判断 ![]() ______(填是或不是)“1阶倒差数”,第5个“2阶倒差数”是______
______(填是或不是)“1阶倒差数”,第5个“2阶倒差数”是______
(2)若![]() 均是由两连续奇数组成的“2阶倒差数”,且
均是由两连续奇数组成的“2阶倒差数”,且![]() .求
.求![]() 的值.
的值.
参考答案:
【答案】(1)是;![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(l) 根据已知中的新定义判断即可;
(2) 根据已知中的新定义首先转化成一般的运算,然后列出方程计算即可求解;
(1)∵![]() ,∴
,∴![]() 是“1阶倒差数”
是“1阶倒差数”
第5个“2阶倒差数”是![]()
故答案为:是;![]()
(2)解:设![]() ,
,![]() ,(其中
,(其中![]() 为奇数)
为奇数)
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() 为奇数
为奇数
∴![]() 、
、![]() 都是偶数
都是偶数
从而可得![]()
∴![]()
∴![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.求证:∠1=∠2.

证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴ ∠1=∠2( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知 A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式:
 .
.(1)求A,B,C三点的坐标;
(2)如果在第二象限内有一点P(m,
 ),若四边形ABOP的面积与三角形ABC 的面积相等,求点P的坐标.
),若四边形ABOP的面积与三角形ABC 的面积相等,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣2+7﹣(﹣3)﹣2
(2)(﹣4)×5+(﹣120)÷6
(3)9
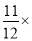 (﹣12)+35.5×4﹣5.5×4
(﹣12)+35.5×4﹣5.5×4(4)﹣22
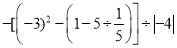
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小明把5÷5÷5记作f(3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f(4,﹣2)
(1)直接写出计算结果,f(5,
 )= ,f(6,3)= ;
)= ,f(6,3)= ;(2)关于“有理数的除方”下列说法正确的是 (填序号)
①对于任何正整数n,都有f(n,﹣1)=1;
②f(6,3)=f(3,6);
③f(2,a)=1(a≠0);
④对于任何正整数n,都有f(2n,a)<0(a<0).
(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式.请推导出“除方”的运算公式f(n,a)(n为正整数,a≠0,n≥2),要求写出推导过程将结果写成幂的形式(结果用含a,n的式子表示)
(4)请利用(3)问的推导公式计算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形
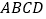 中,
中, ,
,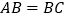 .
.(1)如图1.连接
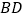 ,若
,若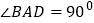 ,求证:
,求证: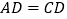 .
.(2)如图2,点
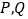 分别在线段
分别在线段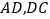 上,满足
上,满足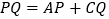 ,求证:
,求证: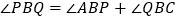 ;
;(3)若点
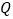 在
在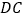 的延长线上,点
的延长线上,点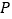 在
在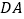 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足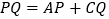 ,请写出
,请写出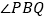 与
与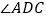 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.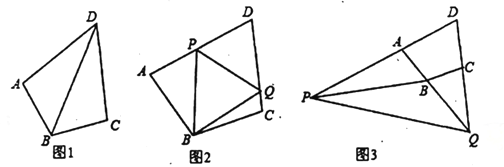
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B、C、D四点所表示的数分别是a、b、c、d,且(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|.
(1)求a、b、c、d的值;
(2)点A,B沿数轴同时出发相向匀速运动,4秒后两点相遇,点B的速度为每秒2个单位长度,求点A的运动速度;
(3)A,B两点以(2)中的速度从起始位置同时出发,向数轴正方向运动,与此同时,C点以每秒1个单位长度的速度向数轴正方向开始运动,若t秒时有2AB=CD,求t的值;
(4)A,B两点以(2)中的速度从起始位置同时出发,相向而行当A点运动到C点时,迅速以原来速度的2倍返回,到达出发点后,保持改变后的速度又折返向C点运动;当B点运动到A点的起始位置后停止运动.当B点停止运动时,A点也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
相关试题

