【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1 , N关于BC的对称点为N2 , 求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
参考答案:
【答案】
(1)
解:由已知,设抛物线解析式为y=a(x﹣2)2
把D(0,﹣1)代入,得a=﹣ ![]()
∴y=﹣ ![]() (x﹣2)2
(x﹣2)2
(2)
解:如图1,连结BN.

∵N1,N2是N的对称点
∴BN1=BN2=BN,∠N1BD=∠NBD,∠NBC=∠N2BC
∴∠N1BN2=2∠DBC
∵四边形ABCD是菱形
∴AB=BC,∠ABC=2∠DBC
∴∠ABC=∠N1BN2, ![]()
∴△ABC∽△N1BN2
(3)
解:∵点N是CD上的动点,
∴点到直线的距离,垂线段最短,
∴当BN⊥CD时,BN最短.
∵C(2,0),D(0,﹣1)
∴CD= ![]() ,
,
∴BNmin= ![]() =
= ![]() ,
,
∴BN1min=BNmin= ![]() ,
,
∵△ABC∽△N1BN2
∴ ![]() ,
,
N1N2min= ![]() ,
,
(4)
解:如图2,

过点P作PE⊥x轴,交AB于点E.
∵∠PQA=∠BAC
∴PQ1∥AC
∵菱形ABCD中,C(2,0),D(0,﹣1)
∴A(﹣2,0),B(0,1)
∴lAB:y= ![]() x+1
x+1
不妨设P(m,﹣ ![]() (m﹣2)2),则E(m,
(m﹣2)2),则E(m, ![]() m+1)
m+1)
∴PE= ![]() m2﹣
m2﹣ ![]() m+2
m+2
∴当m=1时, ![]() ,
,
∴P(1,﹣ ![]() ),
),
∴Q1(﹣ ![]() ,﹣
,﹣ ![]() ).
).
此时,PQ1最小,最小值为 ![]() =
= ![]() ,
,
∴PQ1=PQ2= ![]() .
.
设Q2(n, ![]() n+1),
n+1),
∵P(1,﹣ ![]() ),
),
∴PQ2= ![]() =
= ![]() ,
,
∴n=﹣ ![]() 或n=
或n= ![]() ,
,
∴Q2( ![]() ,
, ![]() ),
),
∴满足条件的Q(﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】(1)用待定系数法求,即可;(2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可;(3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可;(4)先建立PE= ![]() m2﹣
m2﹣ ![]() m+2函数解析式,根据抛物线的特点确定出最小值.
m+2函数解析式,根据抛物线的特点确定出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O中,点A为
 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P. 
(1)求证:PA是⊙O的切线;
(2)若 ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9
 cm2 , 则矩形ABCD的周长为( )
cm2 , 则矩形ABCD的周长为( ) 
A.18cm
B.8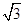 cm
cm
C.(2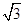 +6)cm
+6)cm
D.(6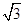 +6)cm
+6)cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组人数的2倍还多1人.从甲组抽调了多少学生去乙组?
【答案】7个人
【解析】
试题设从甲组抽调了
 个学生去乙组,根据抽调后乙组的人数是甲组人数的2倍还多1人即可得出关于
个学生去乙组,根据抽调后乙组的人数是甲组人数的2倍还多1人即可得出关于 的一元一次方程,解之即可得出结论.
的一元一次方程,解之即可得出结论.试题解析:设从甲组抽出
 人到乙组,
人到乙组,




答:从甲组抽调了7名学生去乙组
【题型】解答题
【结束】
26【题目】如图,直线AB和CD交于点O,OE⊥AB,垂足为点O,OP平分∠EOD,∠AOD=144°.
(1)求∠AOC与∠COE的度数;
(2)求∠BOP的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的内接正多边形的一边,已知∠OAB=70°,则这个正多边形的内角和为 .

相关试题

