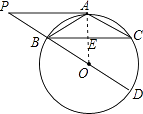
【题目】如图,⊙O中,点A为 ![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P. 
(1)求证:PA是⊙O的切线;
(2)若 ![]() ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值.
参考答案:
【答案】
(1)证明:连结AO,交BC于点E.
∵点A是 ![]() 的中点
的中点
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切线
(2)解:∵AO⊥BC, ![]() ,
,
∴ ![]() ,
,
又∵AB=6
∴ ![]() ,
,
∵OA=OB
∴∠ABD=∠BAO,
∴ ![]() .
.
【解析】(1)根据垂径定理得出AO⊥BC,进而根据平行线的性质得出AP⊥AO,即可证得结论;(2)根据垂径定理得出BE=2 ![]() ,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO=
,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO= ![]() ,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO=
,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO= ![]() .
.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌篮球花费了2400元,购买B品牌篮球花费了1950元,且购买A品牌篮球数量是购买B品牌篮球数量的2倍,已知购买一个B品牌篮球比购买一个A品牌篮球多花50元.
(1)求购买一个A品牌、一个B品牌的篮球各需多少元?
(2)该学校决定再次购进A、B两种品牌篮球共30个,恰逢百货商场对两种品牌篮球的售价进行调整,A品牌篮球售价比第一次购买时提高了10%,B品牌篮球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌篮球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求完成下列题目:
(1)图中有_____块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和左视图与你在图方格中所画的图一致,若这样的几何体最少要m个小正方体,最多要n个小正方体,则m+n的值为____.

【答案】(1)7;(2)画图见解析;(3)16
【解析】
(1)直接根据立体图形得出小正方体的个数;
(2)主视图从左往右小正方形的个数为1,3,2;左视图从左往右小正方形的个数为3,1;俯视图从左往右小正方形的个数1,2,1;
(3)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最少个数和最多个数相加即可.
(1)图中有7块小正方体;
故答案为:7;
(2)如图所示:
 ;
;(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要6个小立方块,最多要10个小立方块.则m+n=16
故答案为:16
【点睛】
此题主要考查了三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形;俯视图决定底层立方块的个数,易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数.
【题型】解答题
【结束】
24【题目】如图,点P是∠AOB的边OA上的一点,作∠AOB的平分线ON;
(1)过点P画OB的平行线交ON于点M;
(2)过点M画OB的垂线,垂足为H;
(3)度量线段PO、PM与MH的长度,会发现:线段PO与PM的大小关系是 ;线段MH与PM的大小关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥纸帽的侧面展开图是一个圆心角为120°,弧长为6π(cm)的扇形纸片,则圆锥形纸帽的侧面积为( )
A.9π cm2
B.18π cm2
C.27π cm2
D.36π cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9
 cm2 , 则矩形ABCD的周长为( )
cm2 , 则矩形ABCD的周长为( ) 
A.18cm
B.8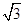 cm
cm
C.(2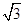 +6)cm
+6)cm
D.(6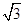 +6)cm
+6)cm -
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组人数的2倍还多1人.从甲组抽调了多少学生去乙组?
【答案】7个人
【解析】
试题设从甲组抽调了
 个学生去乙组,根据抽调后乙组的人数是甲组人数的2倍还多1人即可得出关于
个学生去乙组,根据抽调后乙组的人数是甲组人数的2倍还多1人即可得出关于 的一元一次方程,解之即可得出结论.
的一元一次方程,解之即可得出结论.试题解析:设从甲组抽出
 人到乙组,
人到乙组,




答:从甲组抽调了7名学生去乙组
【题型】解答题
【结束】
26【题目】如图,直线AB和CD交于点O,OE⊥AB,垂足为点O,OP平分∠EOD,∠AOD=144°.
(1)求∠AOC与∠COE的度数;
(2)求∠BOP的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1 , N关于BC的对称点为N2 , 求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
相关试题

