【题目】如图,AB为⊙O的内接正多边形的一边,已知∠OAB=70°,则这个正多边形的内角和为 . 
参考答案:
【答案】1260°
【解析】解:∵OA=OB, ∴∠OAB=∠OBA=70°,
∴∠AOB=40°,
∵AB为⊙O的内接正多边形的一边,
∴正多边形的边数= ![]() =9,
=9,
∴这个正多边形的内角和=(9﹣2)×180°=1260°,
所以答案是:1260°.
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识,掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°,以及对正多边形和圆的理解,了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1 , N关于BC的对称点为N2 , 求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,CA=CB,D为AC上的一点,AD=2CD,AE⊥AB交BD的延长线于E,则
 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )

A.
B.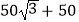
C.
D.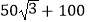
相关试题

