【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为3.
时,该代数式的值为3.
(1)求c的值;
(2)已知:当![]() 时,该代数式的值为0.
时,该代数式的值为0.
①求:当![]() 时,该代数式的值;
时,该代数式的值;
②若![]() ,
,![]() ,
,![]() ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
参考答案:
【答案】(1)c=3;(2)6;a<d.
【解析】
(1)将x=0代入代数式求出c的值即可;
(2)①将x=1代入代数式即可求出a+b的值,再将x=-1代入代数式可得结果;
②根据条件判断a>1,0<d<![]() 或-
或-![]() <d<0,可比较大小.
<d<0,可比较大小.
(1)解:∵当x为0时,代数式![]() 的值为3,
的值为3,
∴ c=3
(2)①∵当![]() 时, 代数式
时, 代数式![]() 的值为0,
的值为0,
∴ a+b+c=0
即a+b与c互为相反数.
∴ a+b=-3.
∴当![]() 时,
时,
![]()
②∵ab>0,且a+b=-3<0,
∴ a<0, b<0.
∵![]() ,
,
∴ a<-1.
∵![]() ,且c=3,
,且c=3,
∴![]() <1.
<1.
∴![]()
∴ a<d.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
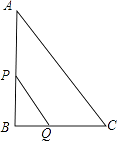
(1)用含x的代数式表示BQ、BP的长度,并求x的取值范围.
(2)设四边形APQC的面积为y(cm2),求y与x的函数关系式?
(3)是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.
?如果存在,求出x的值;不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
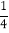 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:点 A、B 在数轴上分别表示两个数 a、b,A、B 两点间的距离记为|AB|,O 表示原点当 A、B 两点中有一点在原点时,不妨设点 A 为原点, 如图 1,则|AB|=|OB|=|b|=|a﹣b|;当 A、B 两点都不在原点时,
①如图 2,若点 A、B 都在原点的右边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②如图 3,若点 A、B 都在原点的左边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=|﹣b﹣(﹣a)=|a﹣b|;
③如图 4,若点 A、B 在原点的两边时,|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|. 回答下列问题:综上所述,数轴上 A、B 两点间的距离为|AB|=|a﹣b|
(1)若数轴上的点 A 表示的数为﹣1,点 B 表示的数为 9,则 A、B 两点间的距离为
(2)若数轴上的点 A 表示的数为﹣1,动点 P 从点 A 出发沿数轴正方向运动, 点 P 的速度是每秒 4 个单位长度,t 秒后点 P 表示的数可表示为
(3)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求:运动几秒时,点 P 可以追上点 Q?(请写出必要的求解过程)

(4)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求运动几秒时,P、Q 两点相距 5 个单位长度?(请写出必要的求解过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
相关试题

