【题目】阅读下面材料:点 A、B 在数轴上分别表示两个数 a、b,A、B 两点间的距离记为|AB|,O 表示原点当 A、B 两点中有一点在原点时,不妨设点 A 为原点, 如图 1,则|AB|=|OB|=|b|=|a﹣b|;当 A、B 两点都不在原点时,
①如图 2,若点 A、B 都在原点的右边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②如图 3,若点 A、B 都在原点的左边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=|﹣b﹣(﹣a)=|a﹣b|;
③如图 4,若点 A、B 在原点的两边时,|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|. 回答下列问题:综上所述,数轴上 A、B 两点间的距离为|AB|=|a﹣b|
(1)若数轴上的点 A 表示的数为﹣1,点 B 表示的数为 9,则 A、B 两点间的距离为
(2)若数轴上的点 A 表示的数为﹣1,动点 P 从点 A 出发沿数轴正方向运动, 点 P 的速度是每秒 4 个单位长度,t 秒后点 P 表示的数可表示为
(3)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求:运动几秒时,点 P 可以追上点 Q?(请写出必要的求解过程)

(4)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求运动几秒时,P、Q 两点相距 5 个单位长度?(请写出必要的求解过程)
参考答案:
【答案】(1)10;(2) 4t﹣1;(3) 运动 5 秒时,点 P 可以追上点 Q;(4) 运动![]() 秒或者
秒或者![]() 秒时,P,Q 两点相距 5 个单位长度
秒时,P,Q 两点相距 5 个单位长度
【解析】
(1)由|AB|=|a﹣b|即可计算;
(2)t 秒后点 P运动的距离为4t,由于P是正方向运动且起点为-1,则P点可表示为4t﹣1;
(3)设运动 x 秒时,点 P 可以追上点 Q,则P的速度为4x,Q的速度为2x,根据题意可知,相遇时P所在的位置为4x﹣1,Q所在的位置为2x+9,据此列方程解答即可;
(4)分点P在点Q左侧和右侧两种情况分别讨论即可.
(1)∵点 A 表示的数为﹣1,点 B 表示的数为 9,
∴|AB|=|﹣1﹣9|=10.
故答案为:10.
(2)∵点 P 运动的速度为每秒4个单位长度,出发点为﹣1,
∴t 秒后点 P 表示的数为 4t﹣1.
故答案为:4t﹣1.
(3)设运动x秒时,点P可以追上点Q,根据题意得:4x﹣1=2x+9,
解得:x=5,
答:运动 5 秒时,点 P 可以追上点 Q.
(4)设运动 y 秒时,P,Q 两点相距 5 个单位长度.
当点 P 在点 Q 左侧时,(2y+9)﹣(4y﹣1)=5,
解得:y=![]() ;
;
当点 P 在点 Q 右侧时,(4y﹣1)﹣(2y+9)=5,解得:y=![]() .
.
答:运动![]() 秒或者
秒或者![]() 秒时,P,Q 两点相距 5 个单位长度.
秒时,P,Q 两点相距 5 个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
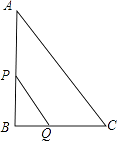
(1)用含x的代数式表示BQ、BP的长度,并求x的取值范围.
(2)设四边形APQC的面积为y(cm2),求y与x的函数关系式?
(3)是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.
?如果存在,求出x的值;不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式
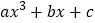 ,当
,当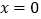 时,该代数式的值为3.
时,该代数式的值为3.(1)求c的值;
(2)已知:当
 时,该代数式的值为0.
时,该代数式的值为0.①求:当
 时,该代数式的值;
时,该代数式的值;②若
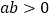 ,
, ,
, ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
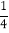 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
相关试题

