【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】C
【解析】
试题已知△ABC、△DCE为正三角形, 故∠DCE=∠BCA=60°,∴∠DCB=60°,
又因为∠DPC=∠DAC+∠BCA,∠BCA=60°,∴∠DPC>60°, 故DP不等于DE,④错.
∵△ABC、△DCE为正三角形, ∴∠ACB=∠DCE=60°,AC=BC,DC=EC, ∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE, ∴△ACD≌△BCE(SAS), ∴∠CAD=∠CBE,AD=BE,故①正确;
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB, ∵∠ACB=∠CBE+∠CEB=60°, ∴∠AOB=60°,故⑤正确;
∵∠ACB=∠DCE=60°, ∴∠BCD=60°, ∴∠ACP=∠BCQ, ∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA), ∴AP=BQ,故③正确.
-
科目: 来源: 题型:
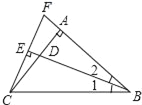
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】桐梓县“四抓四到位”确保教育均衡发展,加速城区新、扩建项目工程,加快建设某间小学,公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的2倍,甲、乙两队合作完成建校工程需要60天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若甲、乙两队共同工作了10天后,乙队因其他工作停止施工,由甲队单独继续施工,要使甲队总的工作量不少于乙队已做工作量的2倍,那么甲队至少再单独施工多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
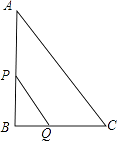
(1)用含x的代数式表示BQ、BP的长度,并求x的取值范围.
(2)设四边形APQC的面积为y(cm2),求y与x的函数关系式?
(3)是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.
?如果存在,求出x的值;不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式
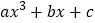 ,当
,当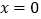 时,该代数式的值为3.
时,该代数式的值为3.(1)求c的值;
(2)已知:当
 时,该代数式的值为0.
时,该代数式的值为0.①求:当
 时,该代数式的值;
时,该代数式的值;②若
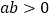 ,
, ,
, ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
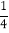 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

相关试题

