【题目】已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程![]() 的两个根,点C在
的两个根,点C在![]() 轴正半轴上,且OB=2OC.
轴正半轴上,且OB=2OC.
(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到![]() ,求直线
,求直线![]() 的表达式.
的表达式.

参考答案:
【答案】(1) A(1,0)、B(4,0)、 C(0,2); (2) ![]()
【解析】
(1)先利用因式分解法解方程x2-5x+4=0可确定A(1,0)、B(4,0);再利用OB=2OC,且点C在y轴正半轴上可确定C点坐标;
(2)利用旋转的性质得OB=OB=4,OC=OC=2,∠COB=∠C0B=90°,∠OCO=∠BCB=90°,则可确定O(-2,2)、B(-2,-2),然后利用待定系数法求直线BC的解析式.
(1) ∵OA、OB的长是方程![]() 2-5
2-5![]() +4=0的两个根,且OA<OB,
+4=0的两个根,且OA<OB,
解得![]()
∴OA=1,OB=4
∵A、B分别在x轴正半轴上,
∴A(1,0)、B(4,0)
又∵OB![]() 2OC,且点C在
2OC,且点C在![]() 轴正半轴上
轴正半轴上
∴OC![]() 2,C(0,2)
2,C(0,2)
(2) ∵ 将△OBC绕点C顺时针旋转90°后得到![]()
∴OB=OB=4,OC=OC=2,∠COB=∠C0B=90°,∠OCO=∠BCB=90°
∴O(-2,2)、B(-2,-2)
设直线BC的解析式为![]()
∴![]() ,解得
,解得![]()
∴直线BC的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.

(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形.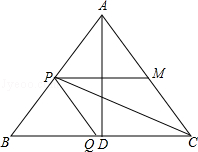
①若a= ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣
 x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).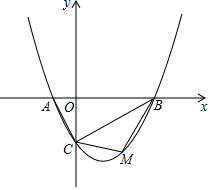
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
-
科目: 来源: 题型:
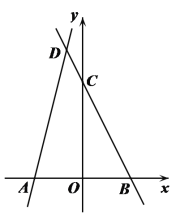
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(-3,0),点B在
 轴上,直线y=-2x+a经过点B与
轴上,直线y=-2x+a经过点B与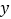 轴交于点
轴交于点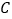 (0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).
(0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).(1)求直线AD的表达式;
(2)点M是直线y=-2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明计划三天看完一本书,预计第一天看 x 页,第二天看的页数比第一天看的页数多50 页,第三天看的页数比第二天看的页数的一半还少5页.
(1)用含x的式子表示这本书的页数;
(2)若 x=100,则这本书共有多少页?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合.
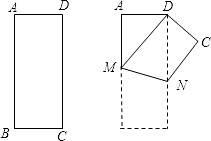
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
相关试题

