【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合. 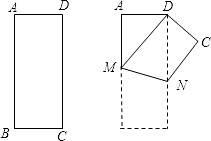
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
参考答案:
【答案】
(1)证明:由题意知∠1=∠2,
又AB∥CD,得∠1=∠3,
则∠2=∠3.
故DM=DN
(2)解:当AB= ![]() AD时,△DMN是等边三角形.
AD时,△DMN是等边三角形.
证明:连接BD.
∵∠A=90°,AB= ![]() AD,
AD,
∴tan∠ABD= ![]() =
= ![]() ,
,
∴∠ABD=30°.
∵BM=MD,
∴∠ABD=∠MDB=30°,
∴∠BMD=120°.
∴∠1=∠2=60°.
又DM=DN,
∴△DMN是等边三角形.
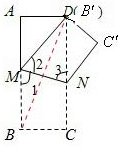
【解析】(1)根据矩形对边平行得∠1=∠3,根据折叠的性质得∠1=∠2,所以∠2=∠3,得DM=DN;(2)假设△DMN是等边三角形,则∠ADM=30°.有MD=2AM,AD= ![]() AM,AB=3AM,得AB=
AM,AB=3AM,得AB= ![]() AD.
AD.
【考点精析】关于本题考查的等边三角形的判定和翻折变换(折叠问题),需要了解三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程
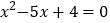 的两个根,点C在
的两个根,点C在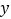 轴正半轴上,且OB=2OC.
轴正半轴上,且OB=2OC.(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到
 ,求直线
,求直线 的表达式.
的表达式.
-
科目: 来源: 题型:
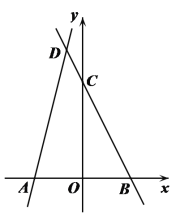
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(-3,0),点B在
 轴上,直线y=-2x+a经过点B与
轴上,直线y=-2x+a经过点B与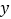 轴交于点
轴交于点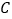 (0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).
(0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).(1)求直线AD的表达式;
(2)点M是直线y=-2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明计划三天看完一本书,预计第一天看 x 页,第二天看的页数比第一天看的页数多50 页,第三天看的页数比第二天看的页数的一半还少5页.
(1)用含x的式子表示这本书的页数;
(2)若 x=100,则这本书共有多少页?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=x与双曲线y=
 相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
相交于点A(a,2),将直线l1向上平移3个单位得到l2 , 直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点. 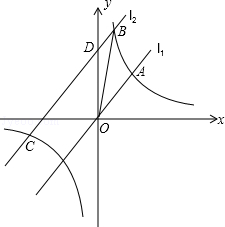
(1)求双曲线y= 的解析式;
的解析式;
(2)求tan∠DOB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州国际动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?
相关试题

