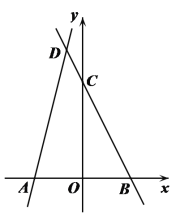
【题目】如图,抛物线y=ax2﹣ ![]() x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).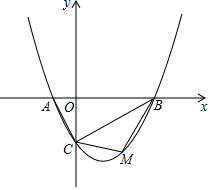
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
参考答案:
【答案】
(1)
解:将B(4,0)代入抛物线的解析式中,得:
0=16a﹣ ![]() ×4﹣2,即:a=
×4﹣2,即:a= ![]() ;
;
∴抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:可得:B(4,0)、C(0,﹣2),设直线BC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]()
故直线BC的解析式为:y=x﹣2;
设xM=t,则yM= ![]() t2﹣
t2﹣ ![]() t﹣2,yN=
t﹣2,yN= ![]() t﹣2,
t﹣2,
S△MBC=S△CME+S△BEM= ![]() EMON+
EMON+ ![]() EMBN=
EMBN= ![]() EMOB
EMOB
= ![]() (
( ![]() t﹣2﹣
t﹣2﹣ ![]() t2+
t2+ ![]() t+2)×4
t+2)×4
=﹣t2+4t
=﹣(t﹣2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,﹣3)
(3)
解:由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,
即:OC2=OAOB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
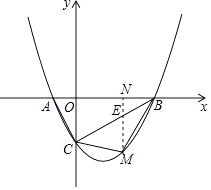
【解析】(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.(2)利用过点M作y轴的平行线,再利用S△MBC=S△CME+S△BEM得出二次函数最值得出答案;(3)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1 , 它与x轴交点为O、A1 , 顶点为P1;将m1绕点A1旋转180°得m2 , 交x轴于点A2 , 顶点为P2;将m2绕点A2旋转180°得m3 , 交x轴于点A3 , 顶点为P3 , …,如此进行下去,直至得m10 , 顶点为P10 , 则P10的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
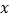 的方程
的方程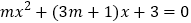 .
.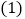 求证:不论
求证:不论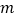 为任何实数,此方程总有实数根;
为任何实数,此方程总有实数根;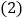 若方程
若方程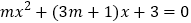 有两个不同的整数根,且
有两个不同的整数根,且 为正整数,求
为正整数,求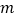 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.

(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形.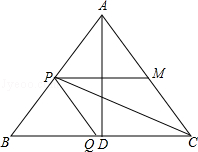
①若a= ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程
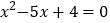 的两个根,点C在
的两个根,点C在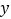 轴正半轴上,且OB=2OC.
轴正半轴上,且OB=2OC.(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到
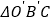 ,求直线
,求直线 的表达式.
的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(-3,0),点B在
 轴上,直线y=-2x+a经过点B与
轴上,直线y=-2x+a经过点B与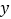 轴交于点
轴交于点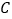 (0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).
(0, 6),直线AD与直线y=-2x+a相交于点D(-1,n).(1)求直线AD的表达式;
(2)点M是直线y=-2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
相关试题

