【题目】已知:如图,点E、F分别是AB、CD上的点,DE、AF分别交BC于G、H,∠A=∠D,∠1=∠2,试说明∠B=∠C.阅读下面的解题过程,在横线上补全推理过程或依据.
解:∵∠1=∠2(已知)
∠1=∠3(______________________________)
∴∠2=∠3(等量代换)
∴AF∥DE(_____________________________)
∴∠4=∠D(__________________________________)
又∵∠A=∠D (已知)
∴∠4=∠A(等量代换)
![]() ______(____________________________________)
______(____________________________________)
∴∠B=∠C (_________________________________)

参考答案:
【答案】对顶角相等 同位角相等,两直线平行 两直线平行,同位角相等 AB∥CD 内错角相等,两直线平行 两直线平行,内错角相等
【解析】
本题主要考查平行线的判定以及性质,根据内错角相等,同位角相等即可判定平行,反之推角等.
由图示可知∠1,∠3关系为对顶角,对顶角性质为相等,故答题空1应填对顶角相等作为依据;
因为∠2,∠3关系为同位角且相等,由其推出平行,故答题空2依据是同位角相等,两直线平行;
因为∠D,∠4关系为同位角,且由AF∥DE推出其相等,故答题空3依据是两直线平行,同位角相等;
因为∠4,∠A关系为内错角且相等,故可推出答题空4为AB∥CD,答题空5依据是内错角相等,两直线平行;
因为∠B,∠C关系为内错角,且由AB∥CD推出其相等,故答题空6依据为两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=
 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
的图象相交于A,B两点,点B的坐标为(2m,﹣m).
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A,B为切点,∠OAB=30度.

(1)求∠APB的度数;
(2)当OA=3时,求AP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点
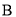 与点E,点
与点E,点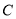 与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D,点
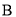 与点E,点
与点E,点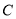 与点F的坐标,并说说对应点的坐标有哪些特征;
与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点
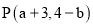 与点
与点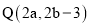 也是通过上述变换得到的对应点,求
也是通过上述变换得到的对应点,求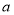 、b的值
、b的值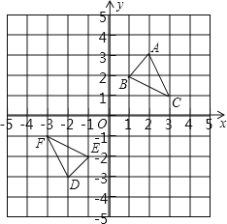
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用若干块图①所示的长方形和正方形硬纸片可以拼出一些新的长方形,并用不同的方法计算它的面积,从而得到相应的等式.计算图②的面积可以得到等式
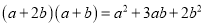 .
.①
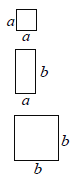 ②
②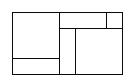
(1)计算图③的面积,可以得到等式__________;
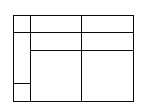 ③
③(2)在虚线框中用图①所示的长方形和正方形硬纸片若干块(每种至少用一次),拼成一个长方形,使拼出的长方形面积为
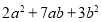 ,并把二次三项式
,并把二次三项式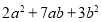 分解因式.
分解因式.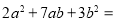 _______________________;
_______________________;(3)如图④,大正方形的边长为
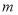 ,小正方形的边长为
,小正方形的边长为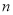 ,若用
,若用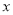 、
、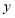 表示四个长方形的长和宽(
表示四个长方形的长和宽(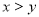 ),观察图形,指出以下关系式正确的有__________个.
),观察图形,指出以下关系式正确的有__________个.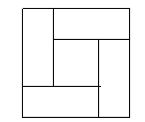

(a)
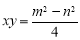 (b)
(b)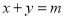
(c)
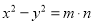 (d)
(d)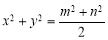
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
相关试题

