【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
参考答案:
【答案】
(1)解:将A(﹣1,0),B(3,0)代入得: ![]() ,
,
解得:b=﹣2,c=﹣3.
抛物线的解析式为y=x2﹣2x﹣3
(2)解:由x=﹣ ![]() 得;抛物线的对称轴为x=1.
得;抛物线的对称轴为x=1.
设点P的坐标为(a,a2﹣2a﹣3).
设直线PA的解析式为y=kx+b.
将点P和点A的坐标代入得: ![]() ,解得:k=a﹣3,b=a﹣3.
,解得:k=a﹣3,b=a﹣3.
∴直线PA的解析式为y=(a﹣3)x+a﹣3.
将x=1代入得:y1=2a﹣6.
设直线PB的解析式为y=k1x+b1.
将点P和点B的坐标代入得: ![]() ,解得:k=a+1,b=﹣3a﹣3.
,解得:k=a+1,b=﹣3a﹣3.
∴直线PB的解析式为y=(a+1)x﹣3a﹣3.
将x=1代入得:y2=﹣2a﹣2.
∴y1+y2=﹣8.
(3)解:如图所示:
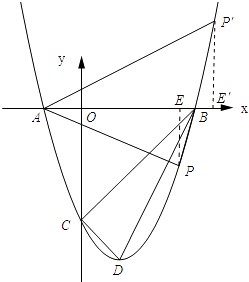
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4).
∵将x=0代入抛物线的解析式得;y=﹣3,
∴C(0,﹣3).
由两点间的距离公式可知:BC=3 ![]() ,DC=
,DC= ![]() ,BD=2
,BD=2 ![]() .
.
∵BC2+DC2=BD2,
∴△BCD为直角三角形.
∴tan∠CBD= ![]() =
= ![]() .
.
设点P的坐标为(a,a2﹣2a﹣3).
∵∠PAB=∠CBD,
∴ ![]() =
= ![]() .
.
整理得:a﹣3= ![]() .
.
解得:a=3 ![]() 或a=2
或a=2 ![]() .
.
∴当a=2 ![]() 时,a+1=
时,a+1= ![]() ,则a2﹣2a﹣3=
,则a2﹣2a﹣3= ![]() =﹣
=﹣ ![]() .
.
∴点P的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
当a= ![]() 时,a+1=
时,a+1= ![]() ,则a2﹣2a﹣3=
,则a2﹣2a﹣3= ![]() =
= ![]() .
.
∴点P′的坐标为( ![]() ,
, ![]() ).
).
综上所述,点P的坐标为( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】(1)用待定系数法,把A(﹣1,0),B(3,0)代入抛物线,求出抛物线的解析式;(2)由抛物线的对称轴为x=1,得到直线PA的解析式和直线PB的解析式,求出y1+y2的值;(3)由抛物线的解析式得到抛物线的顶点坐标,求出C点坐标,根据两点间的距离公式求出BC、DC、BD的值,根据勾股定理的逆定理得到△BCD为直角三角形;根据三角函数值求出点P的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E、F分别是AB、CD上的点,DE、AF分别交BC于G、H,∠A=∠D,∠1=∠2,试说明∠B=∠C.阅读下面的解题过程,在横线上补全推理过程或依据.
解:∵∠1=∠2(已知)
∠1=∠3(______________________________)
∴∠2=∠3(等量代换)
∴AF∥DE(_____________________________)
∴∠4=∠D(__________________________________)
又∵∠A=∠D (已知)
∴∠4=∠A(等量代换)
 ______(____________________________________)
______(____________________________________)∴∠B=∠C (_________________________________)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点
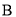 与点E,点
与点E,点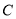 与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D,点
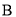 与点E,点
与点E,点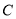 与点F的坐标,并说说对应点的坐标有哪些特征;
与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点
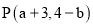 与点
与点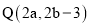 也是通过上述变换得到的对应点,求
也是通过上述变换得到的对应点,求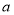 、b的值
、b的值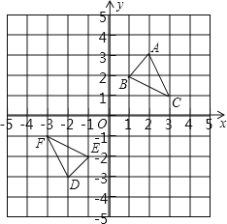
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用若干块图①所示的长方形和正方形硬纸片可以拼出一些新的长方形,并用不同的方法计算它的面积,从而得到相应的等式.计算图②的面积可以得到等式
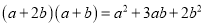 .
.①
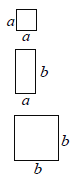 ②
②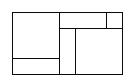
(1)计算图③的面积,可以得到等式__________;
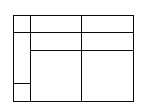 ③
③(2)在虚线框中用图①所示的长方形和正方形硬纸片若干块(每种至少用一次),拼成一个长方形,使拼出的长方形面积为
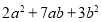 ,并把二次三项式
,并把二次三项式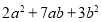 分解因式.
分解因式.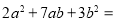 _______________________;
_______________________;(3)如图④,大正方形的边长为
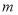 ,小正方形的边长为
,小正方形的边长为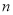 ,若用
,若用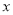 、
、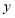 表示四个长方形的长和宽(
表示四个长方形的长和宽(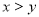 ),观察图形,指出以下关系式正确的有__________个.
),观察图形,指出以下关系式正确的有__________个.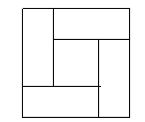

(a)
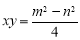 (b)
(b)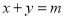
(c)
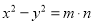 (d)
(d)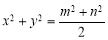
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, ,若动点P从点C开始,按
,若动点P从点C开始,按 的路径运动,且速度为每秒1cm,设出发的时间为t秒.
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
 出发2秒后,求
出发2秒后,求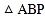 的面积;
的面积; 当t为几秒时,BP平分
当t为几秒时,BP平分 ;
; 问t为何值时,
问t为何值时, 为等腰三角形?
为等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?


-
科目: 来源: 题型:
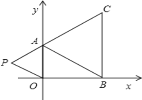
查看答案和解析>>【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
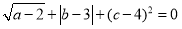 .
.(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,
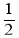 ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
相关试题

