【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
参考答案:
【答案】
(1)证明略
(2)等腰三角形,理由略
【解析】(本小题满分8分)
证明:(1)∵BE=CF,
∴BE+EF=CF+EF, …………1分
即BF=CE. …………………2分
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS), ……………………………………4分
∴AB=DC. ………………………………………5分
(2)△OEF为等腰三角形 …………………………………6分
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC.
∴OE=OF.
∴△OEF为等腰三角形. …………………………………8分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
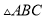 中,
中, 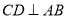 ,垂足为
,垂足为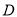 ,点
,点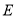 在
在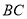 上,
上, 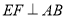 ,垂足为
,垂足为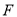 .
.(1)
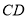 与
与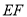 平行吗?为什么?
平行吗?为什么?(2)如果
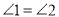 ,且
,且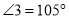 ,求
,求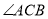 的度数.
的度数.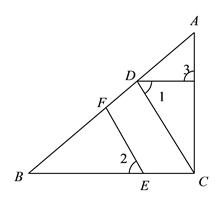
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:
①画出图中△ABC的高AD(标注出点D的位置);
②画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
③根据“图形平移”的性质,得BB1=_____cm,AC与A1C1的位置关系是_____,数量关系是:________.
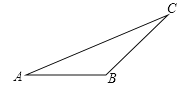
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:因为:∠A=∠F,
所以:_____//______,
理由是:____________,
所以:∠____+∠_____=180°,
理由是:_______________,
因为:∠C=∠D,
所以∠D+∠DEC=180°,
理由是:_________________,
所以:______________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.

(1)求证:AE=CF;
(2)求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.一个游戏的中奖概率是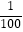 ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据 8,8,7,10,6,8,9 的众数和中位数都是8
D.若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
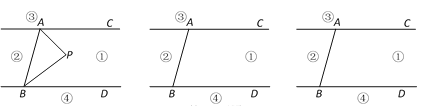
相关试题

