搜索
【题目】阅读理解：
在上学期的学习中，我们知道若
，其中a是底数，n是指数，m称为幂，知道a和n可以求m．我们不妨思考：如果知道a，m，能否求n呢？对于，规定[a，m]=n，例如：
，所以[6，36]=2．
（1）根据上述规定，填空：[3，______]= 4，[2，32]=_____，[-4，1]=______，[5，0.2]=______；
（2）记
，
，求y与x之间的关系式．
参考答案：
【答案】（1）81（或34）；5；0；-1；（2）
．
【解析】
（1）根据乘方、零指数幂、负整数指数幂的性质和新规定求解即可；
（2）根据新规定列式整理即可．
解：（1）∵34＝81，25＝32，
，
，
∴[3，81]= 4，[2，32]=5，[-4，1]=0，[5，0.2]=－1；
故答案为：81；5；0；-1；
（2）由题意得：
，
∴
，即．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙两人匀速从学校出发，相约在某景点见面，甲于8:00出发5分钟后，乙以 a米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s与t的关系示意图一部分如图所示．
根据图中提供的信息回答下列问题：
（1）甲行走的速度为______米/分；
（2）补齐图象，并指出甲到达景点的时刻；
（3）求a的值．
-
科目： 来源： 题型：
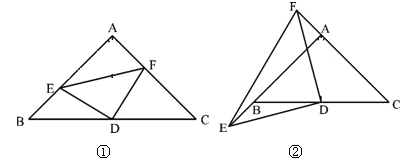
查看答案和解析>>【题目】已知：三角形ABC中，∠A＝90°，AB＝AC，D为BC的中点，
（1）如图①，E，F分别是AB，AC上的点，且BE＝AF，求证：△DEF为等腰直角三角形．
（2）如图②，若E，F分别为AB，CA延长线上的点，仍有BE＝AF，其他条件不变，那么△DEF是否仍为等腰直角三角形？证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学学生步行到郊外旅行，七年级
班学生组成前队，步行速度为4千米
小时，七
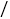班的学生组成后队，速度为6千米小时；前队出发1小时后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回联络，他骑车的速度为10千米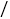小时．后队追上前队需要多长时间？后队追上前队的时间内，联络员走的路程是多少？
七年级班出发多少小时后两队相距2千米？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD∥BC，BE平分∠ABC交AD于点E，BD平分∠EBC．
（1）若∠DBC=35°，则∠A的度数为________；
（2）若∠DBC=α，求∠A的度数（用含α的代数式表示）；
（3）已知120°<∠ABC<180°，若点F在线段AE上，连接BF，当△BFD为直角三角形时，求∠A与∠FBE的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线y=
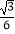x2﹣ 
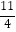x+3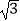 
与x轴交于点A、B两点（点A在点B的左侧），与y轴交于点C，过点C作CD∥x轴，且交抛物线于点D，连接AD，交y轴于点E，连接AC．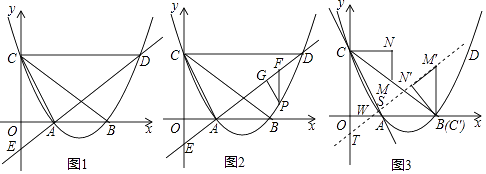
（1）求S△ABD的值；
（2）如图2，若点P是直线AD下方抛物线上一动点，过点P作PF∥y轴交直线AD于点F，作PG∥AC交直线AD于点G，当△PGF的周长最大时，在线段DE上取一点Q，当PQ+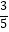
QE的值最小时，求此时PQ+ 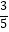QE的值；
（3）如图3，M是BC的中点，以CM为斜边作直角△CMN，使CN∥x轴，MN∥y轴，将△CMN沿射线CB平移，记平移后的三角形为△C′M′N′，当点N′落在x轴上即停止运动，将此时的△C′M′N′绕点C′逆时针旋转（旋转度数不超过180°），旋转过程中直线M′N′与直线CA交于点S，与y轴交于点T，与x轴交于点W，请问△CST是否能为等腰三角形？若能，请求出所有符合条件的WN′的长度；若不能，请说明理由． -
科目： 来源： 题型：
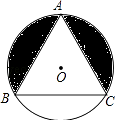
查看答案和解析>>【题目】如图，等边△ABC内接于⊙O，已知⊙O的半径为2，则图中的阴影部分面积为（ ）
A.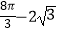
B.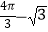
C.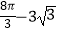
D.4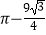
相关试题
