搜索
【题目】如图，等边△ABC内接于⊙O，已知⊙O的半径为2，则图中的阴影部分面积为（ ）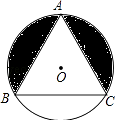
A.
B.
C.
D.4 
参考答案：
【答案】A
【解析】解：连接OB、OC，连接AO并延长交BC于H，则AH⊥BC，
∵△ABC是等边三角形，
∴BH= 
AB= 
，OH=1，
∴△OBC的面积= 
×BC×OH= ，
则△OBA的面积=△OAC的面积=△OBC的面积= ，
由圆周角定理得，∠BOC=120°，
∴图中的阴影部分面积= 
﹣2 = 
π﹣2 ，
所以答案是：A．
【考点精析】掌握等边三角形的性质和三角形的外接圆与外心是解答本题的根本，需要知道等边三角形的三个角都相等并且每个角都是60°；过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
在上学期的学习中，我们知道若
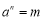，其中a是底数，n是指数，m称为幂，知道a和n可以求m．我们不妨思考：如果知道a，m，能否求n呢？对于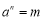，规定[a，m]=n，例如：
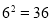，所以[6，36]=2．（1）根据上述规定，填空：[3，______]= 4，[2，32]=_____，[-4，1]=______，[5，0.2]=______；
（2）记
，
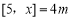，求y与x之间的关系式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD∥BC，BE平分∠ABC交AD于点E，BD平分∠EBC．
（1）若∠DBC=35°，则∠A的度数为________；
（2）若∠DBC=α，求∠A的度数（用含α的代数式表示）；
（3）已知120°<∠ABC<180°，若点F在线段AE上，连接BF，当△BFD为直角三角形时，求∠A与∠FBE的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线y=
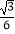x2﹣ 
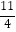x+3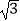 
与x轴交于点A、B两点（点A在点B的左侧），与y轴交于点C，过点C作CD∥x轴，且交抛物线于点D，连接AD，交y轴于点E，连接AC．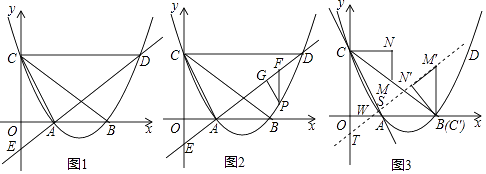
（1）求S△ABD的值；
（2）如图2，若点P是直线AD下方抛物线上一动点，过点P作PF∥y轴交直线AD于点F，作PG∥AC交直线AD于点G，当△PGF的周长最大时，在线段DE上取一点Q，当PQ+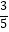
QE的值最小时，求此时PQ+ 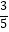QE的值；
（3）如图3，M是BC的中点，以CM为斜边作直角△CMN，使CN∥x轴，MN∥y轴，将△CMN沿射线CB平移，记平移后的三角形为△C′M′N′，当点N′落在x轴上即停止运动，将此时的△C′M′N′绕点C′逆时针旋转（旋转度数不超过180°），旋转过程中直线M′N′与直线CA交于点S，与y轴交于点T，与x轴交于点W，请问△CST是否能为等腰三角形？若能，请求出所有符合条件的WN′的长度；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】同时抛掷两枚质地均匀的骰子，骰子的六个面分别刻有1到6的点数，朝上的面的点数中，一个点数能被另一个点数整除的概率是（ ）
A.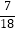
B.
C.
D.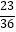
-
科目： 来源： 题型：
查看答案和解析>>【题目】一蓄水池中有水40m3，如果每分钟放出2m3的水，水池里的水量与放水时间有如下关系：
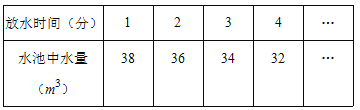
下列数据中满足此表格的是（ ）
A. 放水时间8分钟，水池中水量25m3
B. 放水时问20分钟，水池中水量4m3
C. 放水时间26分钟，水池中水量14m3
D. 放水时间18分钟，水池中水量4m3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图为K90的化学赛道，其中助滑坡AB长90米，坡角a=40°，一个曲面平台BCD连接了助滑坡AB与着陆坡，某运动员在C点飞向空中，几秒之后落在着陆坡上的E处，已知着陆坡DE的坡度i=1：
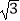，此运动员成绩为DE=85.5米，BD之间的垂直距离h为1米，则该运动员在此比赛中，一共垂直下降了（ ）米．（参考数据：sin40°≈0.64，cos40°≈0.76，tan40°≈0.84，结果保留一位小数）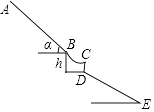
A.101.4
B.101.3
C.100.4
D.100.3
相关试题
