【题目】如图1,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x+3
x+3 ![]() 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.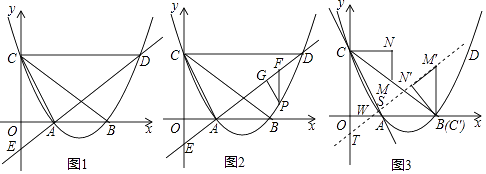
(1)求S△ABD的值;
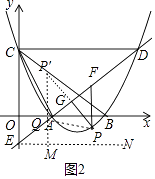
(2)如图2,若点P是直线AD下方抛物线上一动点,过点P作PF∥y轴交直线AD于点F,作PG∥AC交直线AD于点G,当△PGF的周长最大时,在线段DE上取一点Q,当PQ+ ![]() QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+ ![]() QE的值;
QE的值;
(3)如图3,M是BC的中点,以CM为斜边作直角△CMN,使CN∥x轴,MN∥y轴,将△CMN沿射线CB平移,记平移后的三角形为△C′M′N′,当点N′落在x轴上即停止运动,将此时的△C′M′N′绕点C′逆时针旋转(旋转度数不超过180°),旋转过程中直线M′N′与直线CA交于点S,与y轴交于点T,与x轴交于点W,请问△CST是否能为等腰三角形?若能,请求出所有符合条件的WN′的长度;若不能,请说明理由.
参考答案:
【答案】
(1)解:令y=0,则2 ![]() x2﹣33x+36
x2﹣33x+36 ![]() =0,
=0,
解得x= ![]() 或4
或4 ![]() .
.
∴A( ![]() ,0),B(4
,0),B(4 ![]() ,0),C(0,3
,0),C(0,3 ![]() ),
),
∵CD∥AB,
∴S△DAB=S△ABC= ![]() ABOC=
ABOC= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
(2)解:如图2中,设P(m, ![]() m2﹣
m2﹣ ![]() m+3
m+3 ![]() ).
).
∵A( ![]() ,0),D(
,0),D( ![]() ,3
,3 ![]() ),
),
∴直线AD的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
∵PF∥y轴,
∴F(m, ![]() m﹣
m﹣ ![]() ),
),
∵PG⊥DE,
∴△PGF的形状是相似的,
∴PF的值最大时,△PFG的周长最大,
∵PF= ![]() m﹣
m﹣ ![]() ﹣(
﹣( ![]() m2﹣
m2﹣ ![]() m+3
m+3 ![]() )=﹣
)=﹣ ![]() m2+
m2+ ![]() m﹣
m﹣ ![]() ,
,
∴当m=﹣ ![]() =
= ![]() 时,PF的值最大,此时P(
时,PF的值最大,此时P( ![]() ,﹣
,﹣ ![]() ),
),
作P关于直线DE的对称点P′,连接P′Q,PQ,作EN∥x轴,QM⊥EN于M,
∵△QEM∽△EAO,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QM= ![]() QE,
QE,
∴PQ+ ![]() EQ=PQ+QM=P′Q+QM,
EQ=PQ+QM=P′Q+QM,
∴当P′、Q、M共线时,PQ+ ![]() EQ的值最小,
EQ的值最小,
易知直线PP′的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 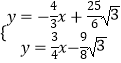 ,可得G(
,可得G( ![]() ,
, ![]() ),
),
∵PG=GP′,
∴P′( ![]() ,
, ![]() ),
),
∴P′M= ![]() +
+ ![]() =
= ![]() ,
,
∴PQ+ ![]() EQ的最小值为
EQ的最小值为 ![]() .
.
(3)解:①如图3中,当CS=CT时,作CK平分∠OCA,作KG⊥AC于G.
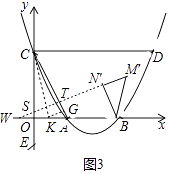
易知KO=KG,
∵ ![]() =
= ![]() =
=  =
= ![]() =
= ![]() ,
,
∴OK= ![]()
![]() =3
=3 ![]() ﹣6
﹣6 ![]() ,
,
易证∠BWN′=∠OCK,
∴tan∠BWN′=tan∠OCK= ![]() =
= ![]() ,
,
∵BN′=2 ![]() ,
,
∴WN′=2 ![]() +4
+4 ![]() .
.
②如图4中,当TC=TS时,
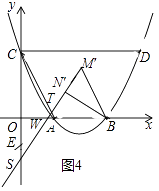
易证∠BWN′=∠OAC,
∴tan∠BWN′=tan∠OAC= ![]() =
= ![]() ,
,
∴WN′= ![]() ,
,
③如图5中,当TS=TC时,延长N′B交直线AC于Q,作BG⊥AQ于G,QR⊥AB于R.

∵TS=TC,
∴∠TSC=∠TCS=∠ACO,
∵∠TSC+∠SQN′=90°,∠ACO+∠OAC=90°,
∴∠BQA=∠OAC=∠BAQ,
∴BA=BQ,
∴AG=GQ,设AQ=a,则易知BG=a,BQ=AB= ![]() a,
a,
∵ ![]() AQBG=
AQBG= ![]() ABQR,
ABQR,
∴QR= a,BR=
![]() a,
a,
∴tan∠WBN′=tan∠QBR= ![]() =
= ![]() ,
,
∴WN′= ![]() .
.
④如图6中,当CS=CT时,
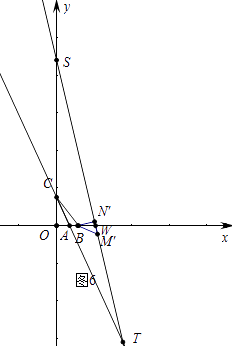
由①可知,在Rt△BN′W中,tan∠N′BW= ![]() =
= ![]() ,
,
∴N′W=2 ![]() ﹣4
﹣4 ![]() .
.
综上所述,满足条件的WN′的长为2 ![]() +4
+4 ![]() 或
或 ![]() 或
或 ![]() 或2
或2 ![]() ﹣4
﹣4 ![]() .
.
【解析】(1)令y=0,代入抛物线的解析式,求出A,B,C的坐标,由CD∥AB,推出S△DAB=S△ABC,由此即可解决问题;
(2)首先说明PF的值最大时,△PFG的周长最大,然后说明当当m=-![]() =
= ![]()
![]() 时,PF的值最大,此时P(
时,PF的值最大,此时P(![]()
![]() ,
,![]()
![]() ),作P关于直线DE的对称点P′,连接P′Q,PQ,作EN∥x轴,QM⊥EN于M,由△QEM∽△EAO对应边成比例推出QM=
),作P关于直线DE的对称点P′,连接P′Q,PQ,作EN∥x轴,QM⊥EN于M,由△QEM∽△EAO对应边成比例推出QM= ![]() QE,推出PQ+
QE,推出PQ+ ![]() EQ=PQ+QM=P′Q+QM,推出P,Q,M三点共线时,PQ+
EQ=PQ+QM=P′Q+QM,推出P,Q,M三点共线时,PQ+ ![]() EQ的值最小,易知直线PP′的解析式,联系直线AD的解析式与直线PP′的解析式求出G点的坐标,进而找到P′的坐标,得到P′M的长度即可;
EQ的值最小,易知直线PP′的解析式,联系直线AD的解析式与直线PP′的解析式求出G点的坐标,进而找到P′的坐标,得到P′M的长度即可;
(3)分两种情况讨论:①如图3中,当CS=CT时,作CK平分∠OCA,作KG⊥AC于G,由tan∠BWN′=tan∠OCK构建方程即可解决问题,②如图4中,当TC=TS时,由tan∠BWN′=tan∠OAC构建方程即可解决问题。
【考点精析】本题主要考查了相似三角形的判定与性质和旋转的性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生步行到郊外旅行,七年级
 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米 小时,七
小时,七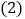 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米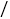 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米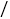 小时.
小时. 后队追上前队需要多长时间?
后队追上前队需要多长时间? 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少? 七年级
七年级 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
在上学期的学习中,我们知道若
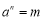 ,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于
,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于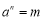 ,规定[a,m]=n,例如:
,规定[a,m]=n,例如: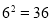 ,所以[6,36]=2.
,所以[6,36]=2.(1)根据上述规定,填空:[3,______]= 4,[2,32]=_____,[-4,1]=______,[5,0.2]=______;
(2)记
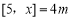 ,
, ,求y与x之间的关系式.
,求y与x之间的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=35°,则∠A的度数为________;
(2)若∠DBC=α,求∠A的度数(用含α的代数式表示);
(3)已知120°<∠ABC<180°,若点F在线段AE上,连接BF,当△BFD为直角三角形时,求∠A与∠FBE的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
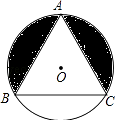
A.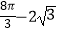
B.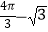
C.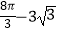
D.4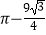
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷两枚质地均匀的骰子,骰子的六个面分别刻有1到6的点数,朝上的面的点数中,一个点数能被另一个点数整除的概率是( )
A.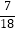
B.
C.
D.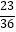
-
科目: 来源: 题型:
查看答案和解析>>【题目】一蓄水池中有水40m3,如果每分钟放出2m3的水,水池里的水量与放水时间有如下关系:
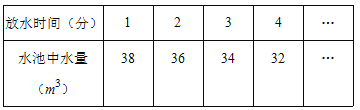
下列数据中满足此表格的是( )
A. 放水时间8分钟,水池中水量25m3
B. 放水时问20分钟,水池中水量4m3
C. 放水时间26分钟,水池中水量14m3
D. 放水时间18分钟,水池中水量4m3
相关试题

